题目内容
3. 如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )
如图,在直角△BAD中,延长斜边BD到点C,使DC=$\frac{1}{2}$BD,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
分析 延长AD,过点C作CE⊥AD,垂足为E,由tanB=$\frac{5}{3}$,即$\frac{AD}{AB}$=$\frac{5}{3}$,设AD=5x,则AB=3x,然后可证明△CDE∽△BDA,然后相似三角形的对应边成比例可得:$\frac{CE}{AB}=\frac{DE}{AD}=\frac{CD}{BD}=\frac{1}{2}$,进而可得CE=$\frac{3}{2}$x,DE=$\frac{5}{2}x$,从而可求tan∠CAD=$\frac{EC}{AE}$=$\frac{1}{5}$.
解答  解:如图,延长AD,过点C作CE⊥AD,垂足为E,
解:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=$\frac{5}{3}$,即$\frac{AD}{AB}$=$\frac{5}{3}$,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴$\frac{CE}{AB}=\frac{DE}{AD}=\frac{CD}{BD}=\frac{1}{2}$,
∴CE=$\frac{3}{2}$x,DE=$\frac{5}{2}x$,
∴AE=$\frac{15}{2}x$,
∴tan∠CAD=$\frac{EC}{AE}$=$\frac{1}{5}$.
故选D.
点评 本题考查了锐角三角函数的定义,相似三角形的判定和性质以及直角三角形的性质,是基础知识要熟练掌握,解题的关键是:正确添加辅助线,将∠CAD放在直角三角形中.

练习册系列答案
相关题目
18.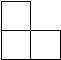 小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
 小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )
小红在观察由一些相同小立方块搭成的几何体时,发现它的主视图、俯视图、左视图均为如图,则构成该几何体的小立方块的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
12.已知甲、乙两地相距20千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
| A. | t=20v | B. | t=$\frac{20}{v}$ | C. | t=$\frac{v}{20}$ | D. | t=$\frac{10}{v}$ |
13. 如图是一个圆台,它的主视图是( )
如图是一个圆台,它的主视图是( )
 如图是一个圆台,它的主视图是( )
如图是一个圆台,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,已知长方形纸片ABCD,AB=CD,AD=BC,现将长方形纸片ABCD沿对角线AC对折,使点B落在点E处,试说明DF=EF.
如图,已知长方形纸片ABCD,AB=CD,AD=BC,现将长方形纸片ABCD沿对角线AC对折,使点B落在点E处,试说明DF=EF. 如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.