题目内容
15.用适当的方法解一元二次方程(x+4)2=5(x+4).分析 利用因式分解法的步骤把原方程变形为(x+4)(x-1)=0,再根据x+4=0或x-1=0,即可求出答案.
解答 解:(x+4)2=5(x+4),
(x+4)2-5(x+4)=0,
(x+4)(x+4-5)=0,
x+4=0或x-1=0,
解得:x1=-4,x2=1.
点评 此题考查了一元二次方程的解法;只有当方程的一边能够分解成两个一次因式,而另一边是0的时候,才能应用因式分解法解一元二次方程.分解因式时,要根据情况灵活运用学过的因式分解的几种方法.

练习册系列答案
相关题目
6. 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | AC=BC+CE | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | ∠A与∠D互余 |
4.永登县明天降雪的概率是30%,对此消息下列说法中中正确的是( )
| A. | 永登县明天将有30%的地区降雪 | B. | 永登县明天将有30%的时间降雪 | ||
| C. | 永登县明天降雪的可能性较小 | D. | 永登县明天肯定不降雪 |
5.若点A的坐标为(1,-2),则下列说法正确的是( )
| A. | 点B(-1,-2)与点A关于x轴对称 | |
| B. | 点A在直线y=5x-3上 | |
| C. | 以点A为圆心,2为半径的圆与y轴相切 | |
| D. | 点A到原点的距离为$\sqrt{5}$ |
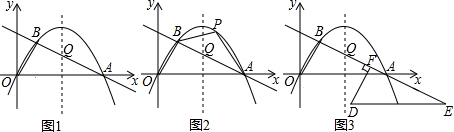

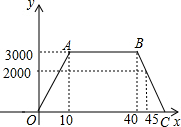 (1)请仔细观察并根据下列函数图,结合生活实际,编一个故事,使故事情境中出现的一对变量x,y满足图示的函数关系式,要求:
(1)请仔细观察并根据下列函数图,结合生活实际,编一个故事,使故事情境中出现的一对变量x,y满足图示的函数关系式,要求: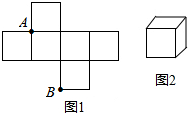 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则在图2中,小虫从点A沿着正方体的棱长爬行到点B的长度为( )
图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则在图2中,小虫从点A沿着正方体的棱长爬行到点B的长度为( )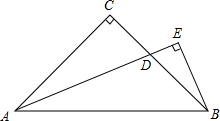 已知,如图在△ABC中,AC=BC,∠C=90°,AD平分∠BAC,BE⊥AE于E.
已知,如图在△ABC中,AC=BC,∠C=90°,AD平分∠BAC,BE⊥AE于E.