题目内容
1. 如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
分析 先利用旋转的性质得CA=CA′,CB=CB′,∠ACA′=∠BCB′=60°,则可判断△ACA′和△BCB′均为等边三角形,于是得到BB′=BC,∠A=60°,∠CBB′=60°,接着计算出∠ABC=90°-∠A=30°,则可计算出BC的长,从而得到BB′的长.
解答 解:∵将△ABC绕点C顺时针旋转60°至△A′B′C,
∴CA=CA′,CB=CB′,∠ACA′=∠BCB′=60°,
∴△ACA′和△BCB′均为等边三角形,
∴BB′=BC,∠A=60°,∠CBB′=60°,
∵点A′在AB上,∠ACB=90°,
∴∠A=60°,∠ABC=90°-∠A=30°,
在Rt△ABC中,BC=$\sqrt{3}$CA=$\sqrt{3}$,
∴BB′=$\sqrt{3}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
11.抛物线y=x2+6x+m与x轴有两个交点,其中一个交点的坐标为(-1,0),那么另一个交点的坐标为( )
| A. | (1,0) | B. | (-5,0) | C. | (-2,0) | D. | (-4,0) |
12.某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如表.(单位:km)
(1)求收工时距A地多远?
(2)在第五次纪录时距A地最远.
(3)若每千米耗油0.3升,问共耗油多少升?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -3 | +8 | -9 | +10 | +4 | -6 | -2 |
(2)在第五次纪录时距A地最远.
(3)若每千米耗油0.3升,问共耗油多少升?
6. 如图,数轴上的A、B、C三点所表示的数分别为a,b,c,其中AB的长度与BC的长度相等,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别为a,b,c,其中AB的长度与BC的长度相等,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
 如图,数轴上的A、B、C三点所表示的数分别为a,b,c,其中AB的长度与BC的长度相等,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别为a,b,c,其中AB的长度与BC的长度相等,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )| A. | 点A的左边 | B. | 点A与点B之间,靠近点A | ||
| C. | 点B与点C之间,靠近点B | D. | 点C的右边 |
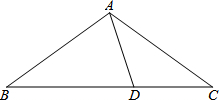 如图,在△ABC中,AB=AC,D为BC上一点,且AB=BD,AD=DC,求∠C的度数.
如图,在△ABC中,AB=AC,D为BC上一点,且AB=BD,AD=DC,求∠C的度数.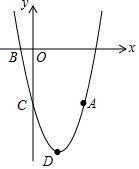 如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.