题目内容
9.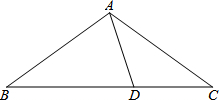 如图,在△ABC中,AB=AC,D为BC上一点,且AB=BD,AD=DC,求∠C的度数.
如图,在△ABC中,AB=AC,D为BC上一点,且AB=BD,AD=DC,求∠C的度数.
分析 设∠C=x,根据等腰三角形的性质,用x表示∠B、∠BAD、∠BDA,再根据三角形内角和定理列出方程即可解决问题.
解答 解:设∠C=x.
∵AB=AC,
∴∠B=∠C=x,
∵AD=DC,
∴∠DAC=∠C=x,
∴∠BDA=∠DAC+∠C=2x,
∵AB=BD
∴∠BAD=∠BDA=2x,
在△ABD中,∠B+∠BAD+∠BDA=x+2x+2x=180°,
解得x=36°
∴∠C=36°.
点评 本题考查等腰三角形的性质,解题的关键是灵活运用等腰三角形的性质解决问题,学会利用参数,构建方程解决问题,属于中考常考题型.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
20.下列说法正确的是( )
| A. | 2a与-3b是同类项 | B. | 0.5x3y2和7x2y3是同类项 | ||
| C. | -a3b2和$\frac{4}{3}$b2a3是同类项 | D. | $\frac{2}{3}$xyz与$\frac{2}{3}$xy是同类项 |
17.下列说法不正确的是( )
| A. | 多项式5x2+4x-2的项是5x2,4x,-2 | B. | 多项式x2-2x+3是二次三项式 | ||
| C. | 2×3,$\frac{a+b}{3}$,$\frac{ab}{2}$,$\frac{3a}{π}$都是单项式 | D. | 3-4a中,一次项的系数是-4 |
4.下列四个有理数中,既是分数又是正数的是( )
| A. | 3 | B. | -3$\frac{1}{2}$ | C. | 0 | D. | 2.4 |
14.下列各式中,不是整式的是( )
| A. | 6ab | B. | $\frac{b}{a}$ | C. | a+1 | D. | 0 |
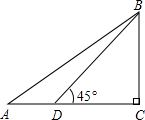 如图,在△ABC,∠C=90°,sin A=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,BD=6$\sqrt{2}$,求AB的长.
如图,在△ABC,∠C=90°,sin A=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,BD=6$\sqrt{2}$,求AB的长. 如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.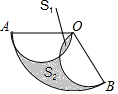 如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π.
如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π.