题目内容
10.计算下列各式:(1)$\frac{1}{x}$+$\frac{1}{2x}$+$\frac{1}{3x}$
(2)3xy2÷$\frac{6{y}^{2}}{x}$
(3)$\frac{2c}{{b}^{2}-{c}^{2}}$-$\frac{1}{b+c}$+$\frac{1}{c-b}$
(4)$\frac{{a}^{2}-4{b}^{2}}{3a{b}^{2}}$•$\frac{ab}{a-2b}$.
分析 根据分式的基本性质即可求出答案.
解答 解:(1)原式=$\frac{6}{6x}$+$\frac{3}{6x}$+$\frac{2}{6x}$=$\frac{11}{6x}$;
(2)原式=3xy2×$\frac{x}{6{y}^{2}}$=$\frac{1}{2}{x}^{2}$;
(3)原式=$\frac{2c}{(b-c)(b+c)}$-$\frac{b-c}{(b+c)(b-c)}$-$\frac{(b+c)}{(b-c)(b+c)}$=$\frac{2c-b+c-b-c}{(b+c)(b-c)}$=$\frac{2c-2b}{(b+c)(b-c)}$=-$\frac{2}{b+c}$;
(4)原式=$\frac{(a-2b)(a+2b)}{3a{b}^{2}}$•$\frac{ab}{a-2b}$=$\frac{a+2b}{3b}$
点评 本题考查分式混合运算,涉及分式的基本性质,因式分解.

练习册系列答案
相关题目
20.下列说法正确的是( )
| A. | 2a与-3b是同类项 | B. | 0.5x3y2和7x2y3是同类项 | ||
| C. | -a3b2和$\frac{4}{3}$b2a3是同类项 | D. | $\frac{2}{3}$xyz与$\frac{2}{3}$xy是同类项 |
5.某冰箱降价30%后,每台售价a元,则该冰箱每台原价应为( )
| A. | 0.3a元 | B. | 0.7a元 | C. | $\frac{10a}{3}$元 | D. | $\frac{10a}{7}$元 |
2.已知x=2是关于x的方程a(x+1)=$\frac{1}{2}$a+x的解,则a的值是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.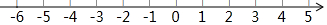 已知关于x的多项式(a+5)x|a|-3+3x-3是二次三项式,一次项系数为b,常数项为c,且a、b、c分别是点A、B、C在数轴上对应的数.
已知关于x的多项式(a+5)x|a|-3+3x-3是二次三项式,一次项系数为b,常数项为c,且a、b、c分别是点A、B、C在数轴上对应的数.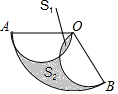 如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π.
如图,扇形OAB中,OA=OB=2,∠AOB=120°,分别以OA,OB为直径画半圆,若图中两个阴影部分面积分别记为S1与S2,则S2-S1的值是$\frac{1}{3}$π.