题目内容
11.抛物线y=x2+6x+m与x轴有两个交点,其中一个交点的坐标为(-1,0),那么另一个交点的坐标为( )| A. | (1,0) | B. | (-5,0) | C. | (-2,0) | D. | (-4,0) |
分析 把(-1,0)代入抛物线y=x2+6x+m求出m的值,再令y=0,求出x的值即可.
解答 解:∵抛物线y=x2+6x+m与x轴的一个交点是(-1,0),
∴1-6+m=0,解得m=5,
∴抛物线的解析式为y=x2+6x+5,
∴令y=0,则x2+6x+5=0,解得x1=-1,x2=-5,
∴另一交点坐标是(-5,0).
故选B.
点评 本题考查的是抛物线与x轴的交点,熟知x轴上点的坐标特点是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
3.下列各算式中,合并同类项正确的是( )
| A. | x2+x2=2x2 | B. | x2+x2=x4 | C. | 2x2-x2=2 | D. | 2x2-x2=2x |
20.下列说法正确的是( )
| A. | 2a与-3b是同类项 | B. | 0.5x3y2和7x2y3是同类项 | ||
| C. | -a3b2和$\frac{4}{3}$b2a3是同类项 | D. | $\frac{2}{3}$xyz与$\frac{2}{3}$xy是同类项 |
 如图,AB是⊙O的弦,C是AB上一点,∠AOC=90°,OA=4,OC=3,求弦AB的长.
如图,AB是⊙O的弦,C是AB上一点,∠AOC=90°,OA=4,OC=3,求弦AB的长.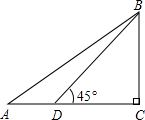 如图,在△ABC,∠C=90°,sin A=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,BD=6$\sqrt{2}$,求AB的长.
如图,在△ABC,∠C=90°,sin A=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,BD=6$\sqrt{2}$,求AB的长. 如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.
如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长.