题目内容
8.在Rt△ABC中,作一个矩形DEGF,其中AC=3cm,BC=4cm,那么矩形DEGF的面积最大是3.分析 设EG=x,则BG=$\frac{4}{3}$x,CE=4-$\frac{4}{3}$x,DE=5-$\frac{16}{12}$x,利用矩形的面积公式即可得到矩形DEFG的面积和x的函数关系,利用函数的性质即可求出其最大值.
解答 解:∵四边形DEFG是矩形,
∴DE∥FG,
∴△CDE∽△ACB,
∴$\frac{DE}{AB}=\frac{CE}{BC}$,
设EG=x,长方形DEGF的面积为y,
则BG=$\frac{4}{3}$x,CE=4-$\frac{4}{3}$x,DE=5-$\frac{16}{12}$x,
矩形面积S=x(5-$\frac{16}{12}$x)=-$\frac{16}{12}$(x-$\frac{6}{5}$)2+3,
∴当x=$\frac{6}{5}$时,矩形的面积最大为3.
故答案为:3.
点评 本题考查了相似三角形的判定和性质以及二次函数的应用,以及二次函数求最值的问题,只要能熟练掌握,便能很容易的解决问题.

练习册系列答案
相关题目
19. 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=6cm,则CD的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=6cm,则CD的长为( )
 如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=6cm,则CD的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=6cm,则CD的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
 如图,已知△ABC,在图中画出:
如图,已知△ABC,在图中画出: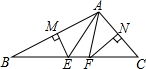 已知:如图,在△ABC中,AB的垂直平分线分别交AB、BC于点M、E,AC的垂直平分线分别交AC、BC于点N、F,∠B=27°,∠BAC=2∠C.求∠EAF的度数.
已知:如图,在△ABC中,AB的垂直平分线分别交AB、BC于点M、E,AC的垂直平分线分别交AC、BC于点N、F,∠B=27°,∠BAC=2∠C.求∠EAF的度数.