题目内容
9．在四边形的4个内角中，钝角的个数最多为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据四边形的内角和为360°以及钝角的定义，用反证法求解．
解答 解：假设四边形的四个内角都是钝角，
那么这四个内角的和＞360°，与四边形的内角和定理矛盾，
所以四边形的四个内角不能都是钝角．
换言之，在四边形的四个内角中，钝角个数最多有3个．
故选C．
点评 本题主要考查了四边形的内角和定理，解决本题的关键是理解四边形的内角和，以及每个内角都是大于0度，并且小于180度．
练习册系列答案
相关题目
19．下列计算中正确的是（ ）
| A． | x3•x2=2x6 | B． | （-3x3）2=-6x6 | C． | （x3）2=x5 | D． | x6÷x2=x4 |
某处欲建一观景平台，如图所示，原设计平台的楼梯长AB=6m，∠ABC=45°，后考虑到安全因素，将楼梯脚B移到CB延长线上点D处，使∠ADC=30°，则调整后楼梯AD的长为6$\sqrt{2}$m．（结果保留根号）
根据下列要求画图．
14．
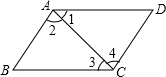如图，要得到AB∥CD，只需要添加一个条件，这个条件不可以是（ ）
如图，要得到AB∥CD，只需要添加一个条件，这个条件不可以是（ ）| A． | ∠1=∠3 | B． | ∠B+∠BCD=180° | C． | ∠2=∠4 | D． | ∠D+∠BAD=180° |
1．
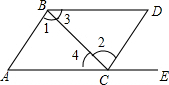如图所示，点E在AC的延长线上，下列条件中不能判断BD∥AE的是（ ）
如图所示，点E在AC的延长线上，下列条件中不能判断BD∥AE的是（ ）| A． | ∠1=∠2 | B． | ∠D+∠ACD=180° | C． | ∠D=∠DCE | D． | ∠3=∠4 |
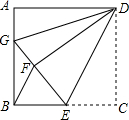如图，正方形ABCD中，AB=12，点E在边BC上，BE=EC，将△DCE沿DE对折至△DFE，延长EF交边AB于点G，连接DG、BF，给出下列结论：①△DAG≌△DFG；②BG=2AG；③△EBF∽△DEG；④S△BEF=$\frac{72}{5}$．其中正确结论的个数是（ ）