题目内容
15.如图①,△ABC是等边三角形,D是△ABC内一点,将△ABD绕点A逆时针旋转60°得到△ACE,连接DE、DC后,可以发现利用旋转变换的不变性,原有的条件发生了转移,使问题得以转化.这种利用“旋转”解决问题的方法在解题中有很多应用,你不妨尝试解决下列问题:如图②,P为正方形ABCD内一点,若PA=α,PB=2α,PC=3α(a为正数),求∠APB的度数.

分析 已知PA=a,PB=2a,PC=3a,并不在同一个三角形中,因为AB=BC,可将△ABP绕点B顺时针方向旋转90°得△CBQ,连接PQ,构成两个特殊三角形,可求∠APB的度数;
解答 解:将△ABP绕点B顺时针方向旋转90°得△CBQ,如图,
则△ABP≌△CBQ且PB⊥QB,
于是PB=QB=2a,PQ=2$\sqrt{2}$a,
在△PQC中,
∵PC2=9a2,PQ2+QC2=9a2,
∴PC2=PQ2+QC2.
∴∠PQC=90°,
∵△PBQ是等腰直角三角形,
∴∠BPQ=∠BQP=45°,故∠APB=∠CQB=90°+45°=135°.
点评 此题主要考查了旋转的性质以及等腰直角三角形的性质,正确应用旋转的性质是解题关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
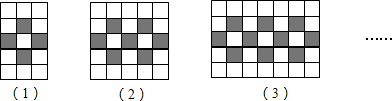
5. 下列四个图案中,能通过如图图案平移得到的是( )
下列四个图案中,能通过如图图案平移得到的是( )
 下列四个图案中,能通过如图图案平移得到的是( )
下列四个图案中,能通过如图图案平移得到的是( )| A. |  | B. |  | C. |  | D. |  |
5.点P(1,2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的A、B、C、D、E、F、G点的坐标.
如图,源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的A、B、C、D、E、F、G点的坐标. 如图1,三角形ABC的各顶点均在格点上,将三角形ABC平移得到三角形A1,B1,C1,使A1点的坐标为(-1,4),
如图1,三角形ABC的各顶点均在格点上,将三角形ABC平移得到三角形A1,B1,C1,使A1点的坐标为(-1,4),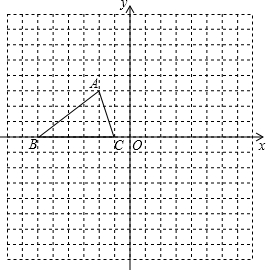 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0),C(-1,0).