题目内容
4. 如图,等边△ABC的边长为2,且DB=DC,∠BDC=120°,现有∠MDN=60°,其两边分别与AB,AC交于点M,N,连接MN,将∠MDN绕着D点旋转,使得M,N始终在边AB和边AC上.试判断在这一过程中,△AMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.
如图,等边△ABC的边长为2,且DB=DC,∠BDC=120°,现有∠MDN=60°,其两边分别与AB,AC交于点M,N,连接MN,将∠MDN绕着D点旋转,使得M,N始终在边AB和边AC上.试判断在这一过程中,△AMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.
分析 不变.要求△AMN的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB至F,使BF=CN,连接DF,通过证明△BDF≌△CND,及△DMN≌△DMF,从而得出MN=MF,△AMN的周长等于AB+AC的长.
解答 解:△AMN的周长没有发生变化,理由如下:
∵△BDC是等腰三角形,且∠BDC=120°,
∴∠BCD=∠DBC=30°,
∵△ABC是边长为3的等边三角形,
∴∠ABC=∠BAC=∠BCA=60°,
∴∠DBA=∠DCA=90°,
延长AB至F,使BF=CN,连接DF,
在△BDF和△CND中,
∵$\left\{\begin{array}{l}{BF=CN}\\{∠FBD=∠DCN}\\{DB=DC}\end{array}\right.$,
∴△BDF≌△CND(SAS),
∴∠BDF=∠CDN,DF=DN,
∵∠MDN=60°,
∴∠BDM+∠CDN=60°,
∴∠BDM+∠BDF=60°,
在△DMN和△DMF中,
∵$\left\{\begin{array}{l}{DM=MD}\\{∠FDM=∠MDN}\\{DF=DN}\end{array}\right.$,
∴△DMN≌△DMF(SAS)
∴MN=MF,
∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=4.
点评 此题考查了旋转的性质,全等三角形的判定与性质,等边三角形的性质;主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.

练习册系列答案
相关题目
9.下列说法正确的是( )
| A. | 零除以任何数都等于零 | |
| B. | 1除以一个数就等于乘这个数的倒数 | |
| C. | 一个不等于零的有理数除以它的相反数等于-1 | |
| D. | 两数相除,商一定小于被除数 |
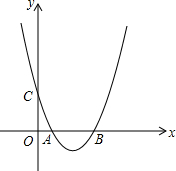 如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4与x轴交于点A、B,与y轴交于点C.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4与x轴交于点A、B,与y轴交于点C. 和
和 ,那么点(
,那么点( ,
,  )在函数
)在函数 图象上的概率是( )
图象上的概率是( ) B.
B.  C.
C.  D.
D. 