题目内容
18.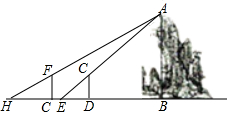 假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G、E、D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.
假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G、E、D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.
分析 首先判定△AEB∽△CED,△AHB∽△FHG,根据相似三角形的性质可得$\frac{AB}{CD}$=$\frac{BE}{DE}$,$\frac{AB}{FG}$=$\frac{BH}{GH}$,再代入数可得答案.
解答  解:由题意得:∠ABD=∠CDE=∠FGH=90°,
解:由题意得:∠ABD=∠CDE=∠FGH=90°,
∵∠CED=∠AEB,∠AHB=∠FHG,
∴△AEB∽△CED,△AHB∽△FHG,
∴$\frac{AB}{CD}$=$\frac{BE}{DE}$,$\frac{AB}{FG}$=$\frac{BH}{GH}$,
即$\frac{AB}{1.5}$=$\frac{2+BD}{2}$,
$\frac{AB}{1.5}$=$\frac{2.4+3.6+BD}{2.4}$,
解得AB=15米,
∴假山的高度AB为15米.
点评 此题主要考查了相似三角形的性质,关键是掌握相似三角形的对边成比例.

练习册系列答案
相关题目
13.“六一”期间,某文具店欲购进A、B两种型号的文具共100只进行销售,其进价和售价之间的关系如表:若该文具店购进A种型号的文具x只,销售完这批文具后所获得的利润为y元.
(1)求y与x的函数关系式;
(2)由于资金紧缺,在实际进货时进货款不得超过1380元,则该文具店销售完这批文具后所能获得最大利润为多少?
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 12 | 18 |
| B型 | 15 | 23 |
(2)由于资金紧缺,在实际进货时进货款不得超过1380元,则该文具店销售完这批文具后所能获得最大利润为多少?
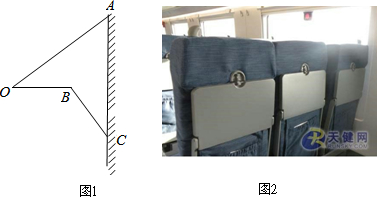
7.如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )


| A. | 40π | B. | 48π | C. | 60π | D. | 80π |
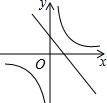
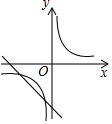
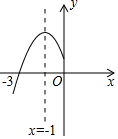 已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax-2b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象大致是( )
已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax-2b与反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象大致是( )