题目内容
2.已知x,y,z均为非负实数,且满足x=5-y+z=1+y+3z,求z的整数解.分析 由已知等式变形表示出x与y,根据x,y,z均为非负实数求出z的范围,确定出z的整数解即可.
解答 解:由x=5-y+z=1+y+3z,得到2y+2z-4=0,
整理得:y=2-z≥0,x=5-2+z+z≥0,
解得:-$\frac{3}{2}$≤z≤2,
当z=0时,x=3,y=2;当z=1时,x=5,y=1;当z=2时,x=7,y=0,
则z的整数解为0,1,2.
点评 此题考查了解二元一次方程,用z表示出x与y是解本题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目


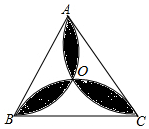 如图,在边长为a的等边三角形ABC中有一个由三个全等的叶形所组成的“三叶草”图形,点O是△ABC的外心,则该“三叶草”图形的面积是$\frac{π}{3}$a2-$\frac{\sqrt{3}}{2}$a2.
如图,在边长为a的等边三角形ABC中有一个由三个全等的叶形所组成的“三叶草”图形,点O是△ABC的外心,则该“三叶草”图形的面积是$\frac{π}{3}$a2-$\frac{\sqrt{3}}{2}$a2. 如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求: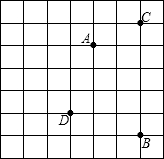 如图,大正方形是由边长为1的小正方形拼成的,A,B,C,D四个点是小正方形的顶点,以其中三个点为顶点,可以构成直角三角形的个数是( )
如图,大正方形是由边长为1的小正方形拼成的,A,B,C,D四个点是小正方形的顶点,以其中三个点为顶点,可以构成直角三角形的个数是( )