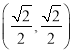Question

【题目】已知一个二次函数图象上部分点的横坐标与纵坐标的对应值如下表所示：

	...						...
	...						...

（1）求这个二次函数的表达式；

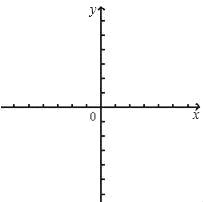
（2）在给定的平面直角坐标系中画出这个二次函数的图象；

（3）结合图像，直接写出当时，的取值范围．

Answer 1

【答案】（1）或；（2）画图见解析；（3）.

【解析】

（1）利用表中数据和抛物线的对称性可得到二次函数的顶点坐标为（1，4），则可设顶点式y=a（x-1）2+4，然后把点（0，3）代入求出a即可；
（2）利用描点法画二次函数图象；
（3）根据x=、3时的函数值即可写出y的取值范围．

解：根据题意可知, 二次函数的顶点坐标为（1，4），

∴设二次函数的解析式为：，

把代入得：；

∴；

∴解析式为：或.

（2）如图所示：

（3）当时，；

当时，；

∵抛物线的对称轴为：，

此时y有最大值4；

∴当时，的取值范围为：.