题目内容
20.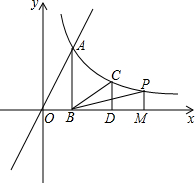 如图,正比例函数y=2x与反比例函数y=$\frac{8}{x}$在第一象限交于点A,过点A作AB⊥x轴于点B.
如图,正比例函数y=2x与反比例函数y=$\frac{8}{x}$在第一象限交于点A,过点A作AB⊥x轴于点B.(1)求点A的坐标;
(2)若点C在y=$\frac{8}{x}$上(x>0),过点C作CD⊥x轴于点D,使S△CBD等于S△AOB的$\frac{2}{3}$,求C点的坐标;
(3)在y=$\frac{8}{x}$上(x>0)是否存在点P,过点P作PM⊥x轴于点M,使△PBM与△AOB相似?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)由正比例函数y=2x与反比例函数y=$\frac{8}{x}$两个解析式组成方程组,解方程即可;
(2)设C点的坐标(x,$\frac{8}{x}$),分两种情况:①当C在点A的右侧时,由三角形的面积关系得出方程$\frac{1}{2}$(x-2)$•\frac{8}{x}$=$\frac{8}{3}$,解方程求出x,即可得出结果;
②当点C在点A的左侧时,由三角形的面积关系得出方程$\frac{1}{2}$(2-x)•$\frac{8}{x}$=$\frac{8}{3}$,解方程求出x,即可得出结果;
(3)设点P坐标为(a,$\frac{8}{a}$),分两种情况:①当$\frac{BM}{AB}=\frac{PM}{OB}$时,得出方程,解方程即可;②当$\frac{BM}{OB}=\frac{PM}{AB}$时,得出方程,解方程即可.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{8}{x}}\end{array}\right.$,得:$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-4}\end{array}\right.$(不合题意舍去),
则A(2,4);
(2)设C点的坐标(x,$\frac{8}{x}$),
∵S△AOB=$\frac{1}{2}$×2×4=4,S△CBD=$\frac{1}{2}$BD•CD=$\frac{2}{3}$×4=$\frac{8}{3}$,
分两种情况:
①当C在点A的右侧时,$\frac{1}{2}$(x-2)$•\frac{8}{x}$=$\frac{8}{3}$,
解得:x=6,
∴$\frac{8}{x}$=$\frac{4}{3}$,
∴C(6,$\frac{4}{3}$);
②当点C在点A的左侧时,$\frac{1}{2}$(2-x)•$\frac{8}{x}$=$\frac{8}{3}$,
解得:x=$\frac{6}{5}$,
∴$\frac{8}{x}=\frac{20}{3}$,
∴C($\frac{6}{5}$,$\frac{20}{3}$);
综上所述:C点的坐标为(6,$\frac{4}{3}$)或($\frac{6}{5}$,$\frac{20}{3}$);
(3)存在点P,使△PBM与△AOB相似,点P的坐标为($\sqrt{17}$+1,$\frac{\sqrt{17}-1}{2}$)或($\sqrt{5}$+1,2$\sqrt{5}$-2).理由如下:
设点P坐标为(a,$\frac{8}{a}$),
∵PM⊥x轴于点M,
∴PMB=90°=∠ABO,
∴分两种情况:
①当$\frac{BM}{AB}=\frac{PM}{OB}$时,$\frac{a-2}{4}=\frac{\frac{8}{a}}{2}$,
解得:a=1±$\sqrt{17}$(负值舍去),
∴a=$\sqrt{17}$+1,$\frac{8}{a}$=$\frac{\sqrt{17}-1}{2}$,
∴P($\sqrt{17}$+1,$\frac{\sqrt{17}-1}{2}$);
②当$\frac{BM}{OB}=\frac{PM}{AB}$时,$\frac{a-2}{2}=\frac{\frac{8}{a}}{4}$,
解得:a=1±$\sqrt{5}$(负值舍去),
∴a=$\sqrt{5}$+1,$\frac{8}{a}$=2$\sqrt{5}$-2,
∴P($\sqrt{5}$+1,2$\sqrt{5}$-2);
综上所述:存在点P,使△PBM与△AOB相似,点P的坐标为($\sqrt{17}$+1,$\frac{\sqrt{17}-1}{2}$)或($\sqrt{5}$+1,2$\sqrt{5}$-2).
点评 本题是反比例函数综合题目,考查了正比例函数和反比例函数解析式的运用、坐标与图形性质、三角形面积的计算方法、相似三角形的判定、解方程等知识;本题综合性强,有一定难度,进行分类讨论是解决问题的关键.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案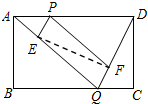 如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )
如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )| A. | y=-$\frac{1}{3}$x2+x | B. | y=-$\frac{2}{3}$x2+2x | C. | y=-$\frac{1}{3}$x2+x+3 | D. | y=-$\frac{2}{3}$x2+2x+6 |
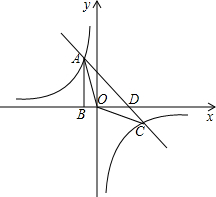 点A是双曲线$y=\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB垂直x轴于点B,且S△ABO=$\frac{3}{2}$;
点A是双曲线$y=\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点,AB垂直x轴于点B,且S△ABO=$\frac{3}{2}$;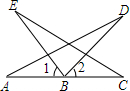 如图,A、B、C在同一条直线上,∠1=∠2,AB=BC,BD=BE.求证:∠D=∠E.
如图,A、B、C在同一条直线上,∠1=∠2,AB=BC,BD=BE.求证:∠D=∠E.