题目内容
12.一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有三张纸牌,牌面数字分别是2、3、4.将纸牌背面朝上充分洗匀,小明和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人摸出一张纸牌,如果所摸球上的数字与纸牌上的数字之和小于5,那么小明去;否则小亮去.(1)求出小明参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.
分析 (1)首先根据题意画出树状图,由树状图求得所有等可能的结果与两指针所指数字之和小于5的情况,则可求得小明参加比赛的概率;
(2)根据小明获胜与小亮获胜的概率,比较概率是否相等,即可判定游戏是否公平;使游戏公平,只要概率相等即可.
解答 解:(1)画树状图得:
∵共有12种等可能的结果,所指数字之和小于5的有3种情况,
∴P(和小于5)=$\frac{3}{12}$=$\frac{1}{4}$,
∴小明参加比赛的概率为:$\frac{1}{4}$;
(2)不公平,
∵P(小明)=$\frac{1}{4}$,
P(小亮)=$\frac{3}{4}$.
∴P(和小于5)≠P(和大于等于5),
∴游戏不公平;
可改为:若两个数字之和小于6,则小明去参赛;否则,小亮去参赛.
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
17.制作合适的统计图表示下列信息:
(1)某城市家庭人口数的统计结果为:2口之家占20%,3口之家占50%,4口之家占10%,5口之家占10%,6口之家占5%,其他占5%.
(2)某市“学生上学方式”抽样调查结果如下:
(3)某家媒体公布世界人口数据为:1957年30亿,1974年40亿,1987年50亿,1999年60亿,2013年70亿,预计2025年80亿.
(1)某城市家庭人口数的统计结果为:2口之家占20%,3口之家占50%,4口之家占10%,5口之家占10%,6口之家占5%,其他占5%.
(2)某市“学生上学方式”抽样调查结果如下:
| 上学方式 | 步行 | 骑自行车 | 乘公共汽车 | 其他 |
| 人数 | 30 | 100 | 150 | 20 |
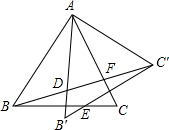 如图,△ABC是正三角形,把△ABC绕点A沿逆时针方向旋转30°得到△AB′C′,边AB′交BC于点D,边B′C′交BC于点E、交AC于点F,其中AB=6
如图,△ABC是正三角形,把△ABC绕点A沿逆时针方向旋转30°得到△AB′C′,边AB′交BC于点D,边B′C′交BC于点E、交AC于点F,其中AB=6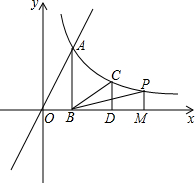 如图,正比例函数y=2x与反比例函数y=$\frac{8}{x}$在第一象限交于点A,过点A作AB⊥x轴于点B.
如图,正比例函数y=2x与反比例函数y=$\frac{8}{x}$在第一象限交于点A,过点A作AB⊥x轴于点B.
 如图,已知:AD∥BC,点E在DC上,且AE,BE分别平分∠BAD和∠ABC.求证:点E为CD中点.
如图,已知:AD∥BC,点E在DC上,且AE,BE分别平分∠BAD和∠ABC.求证:点E为CD中点.