题目内容
15.在平面直角坐标系中将点(3,0),(3,2),(2,3),(2,5),(3,4),(4,5),(4,3),(3,2)用线段依次连接,可以得到一个图形,把这些点的横、纵坐标都乘-1,再将所得的各个点用线段依次连接起来,所得的图形与原图形相比有什么变化?分析 先根据点的坐标的意义描出点(3,0),(3,2),(2,3),(2,5),(3,4),(4,5),(4,3),(3,2),再用线段依次连接,接着再描点(-3,0),(-3,-2),(-2,-3),(-2,-5),(-3,-4),(-4,-5),(-4,-3),(-3,-2),再用线段依次连接,比较两图形的位置可判断它们关于原点中心对称.
解答 解:如图,
所得的图形与原图形关于原点中心对称.
点评 本题考查了坐标与图形性质:利用点的坐标计算相应线段的长和判断线段与坐标轴的位置关系;记住坐标系中特殊位置点的坐标特征.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
5.下列计算结果错误的是( )
| A. | (-a3)2=a6 | B. | a2•a3=a6 | C. | ($\frac{1}{2}$)-1-22=-2 | D. | (cos60°-$\frac{1}{2}$)0=1 |
6.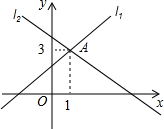 如图直线l1:y=ax+b,与直线l2:y=mx+a交于点A(1,3),那么不等式ax+b<mx+n的解集是( )
如图直线l1:y=ax+b,与直线l2:y=mx+a交于点A(1,3),那么不等式ax+b<mx+n的解集是( )
 如图直线l1:y=ax+b,与直线l2:y=mx+a交于点A(1,3),那么不等式ax+b<mx+n的解集是( )
如图直线l1:y=ax+b,与直线l2:y=mx+a交于点A(1,3),那么不等式ax+b<mx+n的解集是( )| A. | x>3 | B. | x<3 | C. | x>1 | D. | x<1 |
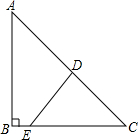 如图所示,某海军基地位于A处,在其正南方向100海里处有一重要目标B,在B的正东方向100海里处也有一重要目标C,小岛D位于AC的中点,岛上有一补给码头,一艘军舰从A出发,经B到C匀速航行,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?
如图所示,某海军基地位于A处,在其正南方向100海里处有一重要目标B,在B的正东方向100海里处也有一重要目标C,小岛D位于AC的中点,岛上有一补给码头,一艘军舰从A出发,经B到C匀速航行,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰,已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇,那么相遇时补给船航行了多少海里(结果精确到0.1海里)?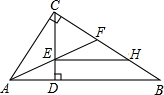 在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠CAB交CD于点F,交CB于点E,过点E作EH∥AB,交BC于H.
在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AE平分∠CAB交CD于点F,交CB于点E,过点E作EH∥AB,交BC于H.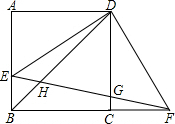 如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线交于点F,连接EF与CD交于点G、与对角线BD相交于点H
如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线交于点F,连接EF与CD交于点G、与对角线BD相交于点H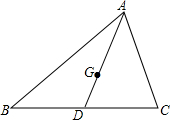 如图,AD为△ABC的中线,G为△ABC的重心,若S△BGC=2,则S△ABD=3.
如图,AD为△ABC的中线,G为△ABC的重心,若S△BGC=2,则S△ABD=3.