Question

11．如图，Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以每秒5cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4cm的速度向点B匀速运动，运动时间为t秒（0＜t＜2），连接PQ．
（1）若△BPQ与△ABC相似，求t的值；
（2）求△BPQ的面积y与t之间的函数关系式；
（3）当t为何值时，△BPQ的面积y有最大值，最大值是多少？

Answer 1

分析 （1）根据勾股定理求出AB，分△BPQ∽△BAC、△BPQ∽△BCA两种情况，根据相似三角形的性质列出比例式，计算即可；
（2）作PE⊥BC于E，根据相似三角形的性质列出比例式，用t表示出PE，根据三角形的面积公式计算即可；
（3）把二次函数的一般式化为顶点式，根据二次函数的性质解答．

解答 解：（1）∵∠ACB=90°，AC=6cm，BC=8cm，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10，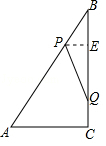
当△BPQ∽△BAC时，$\frac{BP}{BA}$=$\frac{BQ}{BC}$，即$\frac{5t}{10}$=$\frac{8-4t}{8}$，
解得t=1，
当△BPQ∽△BCA时，$\frac{BP}{BC}$=$\frac{BQ}{BA}$，即$\frac{5t}{8}$=$\frac{8-4t}{10}$，
解得，t=$\frac{32}{41}$，
∴当t=1或t=$\frac{32}{41}$时，△BPQ与△ABC相似；
（2）作PE⊥BC于E，
则△BPE∽△BAC，
∴$\frac{BP}{BA}$=$\frac{PE}{AC}$，即$\frac{5t}{10}$=$\frac{PE}{6}$，
解得，PE=3t，
∴y=$\frac{1}{2}$×（8-4t）×3t=-6t²+12t；
（3）y=-6t²+12t=-6（t-1）²+6，
∴t=1，y最大值为6．

点评 本题考查的是相似三角形的性质、二次函数的性质，掌握相似三角形的判定定理和性质定理、熟记二次函数的性质是解题的关键．