Question

20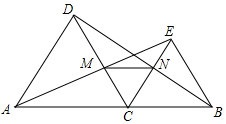．如图，点C是线段AB上除点A、B外的任意一点，分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE，连接AE交DC于M，连接BD交CE于N，连接MN．
（1）求证：AE=BD；
（2）判断△CMN的形状并说明理由．

Answer 1

分析 （1）由等边三角形的性质，结合条件可证明△ACE≌△DCB，则可证得AE=BD；
（2）利用（1）的结论，结合等边三角形的性质可证明△ACM≌△DCN，可证得MC=NC，则可判定△CMN为等边三角形．

解答 （1）证明：
∵△ACD和△BCE是等边三角形，
∴AC=DC，CE=CB，∠DCA=60°，∠ECB=60°，
∵∠DCA=∠ECB=60°，
∴∠DCA+∠DCE=∠ECB+∠DCE，∠ACE=∠DCB，
在△ACE与△DCB中，
$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{CE=CB}\end{array}\right.$
∴△ACE≌△DCB（SAS），
∴AE=BD；
（2）解：△CMN为等边三角形，理由如下：
∵由（1）得，△ACE≌△DCB，
∴∠CAM=∠CDN，
∵∠ACD=∠ECB=60°，而A、C、B三点共线，
∴∠DCN=60°，
在△ACM与△DCN中，
$\left\{\begin{array}{l}{∠MAC=∠NDC}\\{AC=DC}\\{∠ACM=∠DCN}\end{array}\right.$
∴△ACM≌△DCN（ASA），
∴MC=NC，
∵∠MCN=60°，
∴△MCN为等边三角形．

点评 本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．