题目内容
19. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,下列结论一定成立的是( )
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,下列结论一定成立的是( )| A. | AO=BO | B. | ∠BOC=90° | C. | AD=AC | D. | ∠ADO=∠CBO |
分析 利用平行四边形的性质一一判断即可解决问题.
解答 解:A、错误.OA=OC,OA与OB不一定相等;
B、错误.理由平行四边形的对角线不一定垂直;
C、错误.平行四边形的对边相等,AD=BC,AD由AC不一定相等;
D、正确.因为AD∥BC,所以∠ADO=∠CBO;
故选D.
点评 本题考查平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.

练习册系列答案
相关题目
9.邻补角是( )
| A. | 和为180°的两个角 | |
| B. | 有公共顶点且有一条公共边,另一边互为反向延长线的两个角 | |
| C. | 有一条公共边且相等的两个角 | |
| D. | 有公共顶点且互补的两个角 |
7.小李打羽毛球时,若羽毛球飞行的高度h(m)与发球的时间t(s)满足关系式h=-2t2+2t+2,则小李发球后0.5s时,羽毛球飞行的高度为( )
| A. | 1.5m | B. | 2m | C. | 2.5m | D. | 3m |
14.若三角形的两条边的长度是4cm和9cm,则第三条边的长度可能是( )
| A. | 4 cm | B. | 5 cm | C. | 9 cm | D. | 13 cm |
4.下列算式正确的是( )
| A. | $\root{3}{-8}$=-2 | B. | $\sqrt{25}$=±5 | C. | -$\sqrt{49}$=7 | D. | $\sqrt{(-4)^{2}}$=-4 |
11.若关于x的方程ax-b=0(a≠0)的解为x=3,则一次函数y=ax-b(a≠0)的图象与x轴的交点坐标为( )
| A. | (-3,0) | B. | (3,0) | C. | (a,0) | D. | (-b,0) |
9.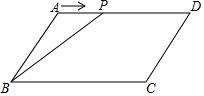 如图,在平行四边形ABCD中,AB=4,∠ABC=60°,动点P从点A开始沿边AD向D点移动(D除外),设P点移动的距离为x,设△ABP的面积为y,则y与x的函数关系式( )
如图,在平行四边形ABCD中,AB=4,∠ABC=60°,动点P从点A开始沿边AD向D点移动(D除外),设P点移动的距离为x,设△ABP的面积为y,则y与x的函数关系式( )
 如图,在平行四边形ABCD中,AB=4,∠ABC=60°,动点P从点A开始沿边AD向D点移动(D除外),设P点移动的距离为x,设△ABP的面积为y,则y与x的函数关系式( )
如图,在平行四边形ABCD中,AB=4,∠ABC=60°,动点P从点A开始沿边AD向D点移动(D除外),设P点移动的距离为x,设△ABP的面积为y,则y与x的函数关系式( )| A. | y=-4x+2 | B. | y=-4x-2 | C. | y=2$\sqrt{3}$x | D. | y=$\sqrt{3}$x |
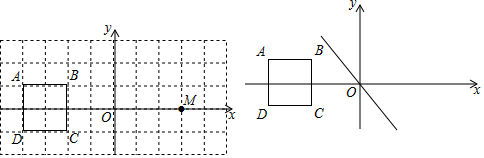
 如图,在长方形ABCD中,AD=12cm,AB=9cm,AE=2BE,DF=2EF,G为FC的中点,则阴影部分的面积是15平方厘米.
如图,在长方形ABCD中,AD=12cm,AB=9cm,AE=2BE,DF=2EF,G为FC的中点,则阴影部分的面积是15平方厘米.