Question

8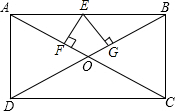．如图所示，在矩形ABCD中，对角线AC，BD交于点O，∠AOD=60°，AB=5，E是AD上任意一点，EF⊥AC于点F，EG⊥BD于点G．
（1）求对角线AC的长，边AD的长；
（2）EF+EG的长随E点的变化而变化吗？若不变化，求出它的值；若变化，请说明理由．

Answer 1

分析 （1）先证明△OBC是等边三角形，得出BC=OC，∠BCA=60°，根据三角函数求出AC，得出AD即可；
（2）证出EF=$\frac{1}{2}$AE，EG=$\frac{1}{2}$BE，得出EF+EG=$\frac{1}{2}$（AE+BE）=$\frac{1}{2}$AB即可．

解答 解：（1）∵四边形ABCD是矩形，
∴∠ABC=∠BAD=90°，AD=BC，OA=OB=OC=OD，
∵∠AOD=60°，
∴△OBC是等边三角形，
∴BC=OC，∠BCA=60°，
∴AC=$\frac{AB}{sin60°}$=$\frac{5}{\frac{\sqrt{3}}{2}}$=$\frac{10\sqrt{3}}{3}$，BC=$\frac{1}{2}$AC=$\frac{5\sqrt{3}}{3}$，
∴AD=$\frac{5\sqrt{3}}{3}$；
（2）EF+EG的长不变化；理由如下：
由（1）得：∠OAB=∠OBA=30°，
∵EF⊥AC于点F，EG⊥BD于点G，
∴EF=$\frac{1}{2}$AE，EG=$\frac{1}{2}$BE，
∴EF+EG=$\frac{1}{2}$（AE+BE）=$\frac{1}{2}$AB=$\frac{5}{2}$．

点评 本题考查了矩形的性质、等边三角形的判定与性质、含30°的直角三角形的性质；熟练掌握矩形的性质，证明三角形是等边三角形是解决问题的关键．