题目内容
18.先化简,再求值:($\frac{4x+6}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{x}^{2}-2x+1}$,其中x是不等式组$\left\{\begin{array}{l}{x+4>0}\\{1-2x>3}\end{array}\right.$的整数解.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出不等式组的解集,找出解集中的整数解确定出x的值,代入计算即可求出值.
解答 解:原式=$\frac{4x+6-2x-2}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+2}$=$\frac{2(x+2)}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+2}$=$\frac{2x-2}{x+1}$,
又$\left\{\begin{array}{l}{x+4>0①}\\{1-2x>3②}\end{array}\right.$,
由①解得:x>-4,
由②解得:x<-1,
故不等式组的解集为-4<x<-1,其整数解为-3,-2,
当x=-3时,原式=4;
当x=-2时,原式无意义.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9.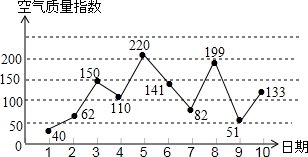 如图是某市11月1日至10日的空气质量指数折线图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月7日中的某一天到达该市旅游,到达的当天作为第一天连续停留4天.则此人在该市停留期间恰好有两天空气质量优良的概率是( )
如图是某市11月1日至10日的空气质量指数折线图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月7日中的某一天到达该市旅游,到达的当天作为第一天连续停留4天.则此人在该市停留期间恰好有两天空气质量优良的概率是( )
 如图是某市11月1日至10日的空气质量指数折线图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月7日中的某一天到达该市旅游,到达的当天作为第一天连续停留4天.则此人在该市停留期间恰好有两天空气质量优良的概率是( )
如图是某市11月1日至10日的空气质量指数折线图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月7日中的某一天到达该市旅游,到达的当天作为第一天连续停留4天.则此人在该市停留期间恰好有两天空气质量优良的概率是( )| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
13.杭州跨境贸易产业园(下沙园区)从去年5月7日开园试点到今年1月26日,园区实现进口业务109万单,其中109万用科学记数法表示为( )
| A. | 109×104 | B. | 10.9×105 | C. | 1.09×106 | D. | 0.109×108 |
3.下列各等式中,错误的是( )
| A. | x+$\frac{1}{x}$=$\frac{1+{x}^{2}}{x}$ | B. | (x-3)2=x2-9 | C. | x2-x=x(x-1) | D. | |x-1|2=(x-1)2 |
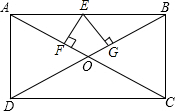 如图所示,在矩形ABCD中,对角线AC,BD交于点O,∠AOD=60°,AB=5,E是AD上任意一点,EF⊥AC于点F,EG⊥BD于点G.
如图所示,在矩形ABCD中,对角线AC,BD交于点O,∠AOD=60°,AB=5,E是AD上任意一点,EF⊥AC于点F,EG⊥BD于点G.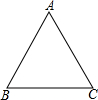 对于边长为10的正三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.
对于边长为10的正三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.