题目内容
2．
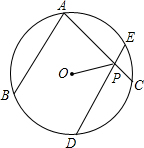如图，已知AB和DE是⊙O的两条弦，且AB∥DE，C为DE上的一点，CD=BD，连接AC交DE于P，连接OP．（1）求证：$\widehat{AC}$=$\widehat{DE}$；
（2）求证：OP平分∠APD．
分析 （1）由AB和DE是⊙O的两条弦，且AB∥DE，可得$\widehat{AE}$=$\widehat{BD}$，又由CD=BD，易证得$\widehat{AE}$=$\widehat{CD}$，继而证得结论；
（2）首先过点O作OM⊥DE于点M，过点O作ON⊥AC于点N，易证得弦心距OM=ON，则可证得OP平分∠APD．
解答 证明：（1）∵AB和DE是⊙O的两条弦，且AB∥DE，
∴$\widehat{AE}$=$\widehat{BD}$，
∵CD=BD，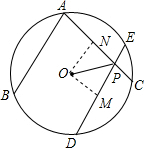
∴$\widehat{CD}$=$\widehat{BD}$，
∴$\widehat{AE}$=$\widehat{CD}$，
∴$\widehat{AE}$+$\widehat{CE}$=$\widehat{CD}$+$\widehat{CE}$，
即$\widehat{AC}$=$\widehat{DE}$；
（2）过点O作OM⊥DE于点M，过点O作ON⊥AC于点N，
∵$\widehat{AC}$=$\widehat{DE}$，
∴AC=DE，
∴OM=ON，
∴OP平分∠APD．
点评 此题考查了弧与弦的关系．注意掌握辅助线的作法．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目