题目内容
17.已知$\frac{{x}^{2}+2xy{+y}^{2}}{xy{-y}^{2}}$÷A=$\frac{xy{+y}^{2}}{{x}^{2}-2xy{+y}^{2}}$,当x=2,y=1时,求A的值.分析 利用A=被除式除以商得出结果,进一步代入求得答案即可.
解答 解:∵$\frac{{x}^{2}+2xy{+y}^{2}}{xy{-y}^{2}}$÷A=$\frac{xy{+y}^{2}}{{x}^{2}-2xy{+y}^{2}}$,
∴A=$\frac{{x}^{2}+2xy{+y}^{2}}{xy{-y}^{2}}$÷$\frac{xy{+y}^{2}}{{x}^{2}-2xy{+y}^{2}}$
=$\frac{(x+y)^{2}}{y(x-y)}$•$\frac{(x-y)^{2}}{y(x+y)}$
=$\frac{{x}^{2}-{y}^{2}}{{y}^{2}}$
当x=2,y=1时,
A=3.
点评 此题考查分式的乘除法,与代数式求值,掌握分式的乘除法是解决问题的关键.

练习册系列答案
相关题目
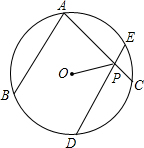 如图,已知AB和DE是⊙O的两条弦,且AB∥DE,C为DE上的一点,CD=BD,连接AC交DE于P,连接OP.
如图,已知AB和DE是⊙O的两条弦,且AB∥DE,C为DE上的一点,CD=BD,连接AC交DE于P,连接OP.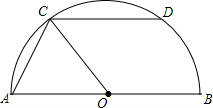 如图,AB是半圆O的直径,CD是半圆O的弦,CD∥AB,连接CO,AC,若∠BOC=124°,求∠ACD的度数.
如图,AB是半圆O的直径,CD是半圆O的弦,CD∥AB,连接CO,AC,若∠BOC=124°,求∠ACD的度数.