题目内容
1.某地生产椪柑,春节期间,一外地运销客户安排15辆汽车装运A,B,C三种不同品质的椪柑120吨到外地销售,按计划15辆汽车都要装满且每辆汽车只能装同一种品质的椪柑,每种椪柑所用车辆都不少于3辆.(1)设装运A种椪柑的车辆数为x辆,装运B种椪柑车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
| 椪柑品种 | A | B | C |
| 每辆汽车运载量(吨) | 10 | 8 | 6 |
分析 (1)设装运A种椪柑的车辆数为x辆,装运B种椪柑车辆数为y辆,则装C种椪柑的车辆是(15-x-y)辆,根据等量关系为:装运A,B,C三种不同品质的椪柑一共120吨,由此可得出x与y的关系式;
(2)关系式为:装运每种脐橙的车辆数≥3,依此即可求解.
解答 解:(1)设装运A种椪柑的车辆数为x辆,装运B种椪柑车辆数为y辆,则装C种椪柑的车辆是(15-x-y)辆.
则10x+8y+6(15-x-y)=120,
即10x+8y+90-6x-6y=120,
则y=15-2x;
(2)根据题意得:
$\left\{\begin{array}{l}{x≥3}\\{15-2x≥3}\\{15-x-(15-2x)≥3}\end{array}\right.$,
解得:3≤x≤6.
故有四种方案:A、B、C三种的车辆数分别是:3辆、9辆、3辆;或4辆、7辆、4辆;或5辆、5辆、5辆;或6辆、3辆、6辆.
点评 本题考查了一次函数的应用及不等式的应用,解决本题的关键是读懂题意,根据关键描述语,找到所求量的等量关系,确定x的范围,得到装在的几种方案是解决本题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
6.菲尔兹奖是国际上有崇高声誉的一个数学奖项,下面的数据是从1936年至2014年菲尔兹奖得主获奖时的年龄(岁):
29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
 请根据上述数据,解答下列问题:
请根据上述数据,解答下列问题:
小彬按“组距为5”列出了如图的频数分布表
(1)每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图;
(2)根据(1)中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征;
(3)在(1)的基础上,小彬又画了如图所示的扇形统计图,图中获奖年龄在30~35岁的人数约占获奖总人数的26.8%(百分号前保留1位小数);C组所在扇形对应的圆心角度数约为199°(保留整数)
29 39 35 33 39 27 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 32
29 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
 请根据上述数据,解答下列问题:
请根据上述数据,解答下列问题:小彬按“组距为5”列出了如图的频数分布表
| 分组 | 频数 |
| A:25~30 | 4 |
| B:30~35 | 15 |
| C:35~40 | 31 |
| D:40~45 | 6 |
| 合计 | 56 |
(2)根据(1)中的频数分布直方图描述这56位菲尔兹奖得主获奖时的年龄的分布特征;
(3)在(1)的基础上,小彬又画了如图所示的扇形统计图,图中获奖年龄在30~35岁的人数约占获奖总人数的26.8%(百分号前保留1位小数);C组所在扇形对应的圆心角度数约为199°(保留整数)
13.在菱形ABCD中,AC,BD为对角线,下列说法一定正确的是( )
| A. | AC=BD | B. | AC⊥BD | C. | ∠ABD=∠BAC | D. | ∠BAC+∠CAD=90° |
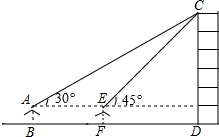 某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)
某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)
 如图放置的正方形ABCD,正方形DCC1D1,正方形D1C1C2D2,…都是边长为$\sqrt{3}$的正方形,点A在y轴上,点B,C,C1,C2,…,都在直线y=$\frac{\sqrt{3}}{3}$x上,则D的坐标是($\sqrt{3}$,1+$\frac{4\sqrt{3}}{3}$),Dn的坐标是($\sqrt{3}$(n+1),$\frac{3(n+1)+4\sqrt{3}}{3}$).
如图放置的正方形ABCD,正方形DCC1D1,正方形D1C1C2D2,…都是边长为$\sqrt{3}$的正方形,点A在y轴上,点B,C,C1,C2,…,都在直线y=$\frac{\sqrt{3}}{3}$x上,则D的坐标是($\sqrt{3}$,1+$\frac{4\sqrt{3}}{3}$),Dn的坐标是($\sqrt{3}$(n+1),$\frac{3(n+1)+4\sqrt{3}}{3}$). 如图,△ABC中,AB=AC,D为BC上一点,CD=DE,证明:A、B、D、E四点共圆.
如图,△ABC中,AB=AC,D为BC上一点,CD=DE,证明:A、B、D、E四点共圆.