题目内容
7.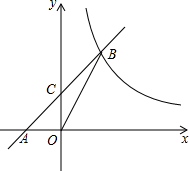 已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若S△AOB=4.
已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象交于点B(2,n),连结BO,若S△AOB=4.(1)求该反比例函数的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
分析 (1)先根据三角形面积公式求出n得到B(2,4),然后利用待定系数法求反比例函数解析式;
(2)先利用待定系数法求出直线AB的解析式,再确定C点坐标,然后利用三角形面积公式求解.
解答 解:(1)∵S△AOB=4,
∴$\frac{1}{2}$×2×n=4,解得n=4,
∴B(2,4),
设反比例函数解析式为y=$\frac{k}{x}$,
把B(2,4)代入得k=2×4=8,
∴反比例函数解析式为y=$\frac{8}{x}$;
(2)设直线AB的解析式为y=ax+b,
把A(-2,0),B(2,4)代入得$\left\{\begin{array}{l}{-2a+b=0}\\{2a+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=x+2,
当x=0时,y=x+2=2,则C(0,2),
∴S△OCB=$\frac{1}{2}$×2×2=2.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法求反比例函数和一次函数解析式.

练习册系列答案
相关题目
17.第一盒乒乓球中有3个白球,1个黄球,第二盒乒乓球中有2个白球,2个黄球,分别从每个盒子中随机地取出1个球,则取出的两个球中有一个白球一个黄球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
15. 如图是一个几何体的三视图,则这个几何体的表面积是( )
如图是一个几何体的三视图,则这个几何体的表面积是( )
 如图是一个几何体的三视图,则这个几何体的表面积是( )
如图是一个几何体的三视图,则这个几何体的表面积是( )| A. | 140 | B. | 280 | C. | 180 | D. | 360 |
16.下列说法中正确的是( )
| A. | 掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为$\frac{1}{2}$ | |
| B. | “对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件 | |
| C. | “同位角相等”这一事件是不可能事件 | |
| D. | “钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件 |
17.下列因式分解正确的是( )
| A. | x2-4=(x+4)(x-4) | B. | x2+2x+1=x(x+2)+1 | C. | 3mx-6my=3m(x-6y) | D. | 2x+4=2(x+2) |
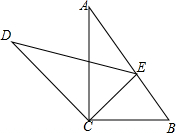 如图,直角三角形ABC中,∠ACB=90°,将△ABC绕点C按逆时针方向旋转α后得到△DEC,此时点E在AB边上,则∠A的度数是$\frac{1}{2}α$(用含α的代数式表示)
如图,直角三角形ABC中,∠ACB=90°,将△ABC绕点C按逆时针方向旋转α后得到△DEC,此时点E在AB边上,则∠A的度数是$\frac{1}{2}α$(用含α的代数式表示) 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.