题目内容
11.某经销店为某工厂代销一种建筑材料(代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).(1)当每吨售价是220元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)据(2)中的函数关系式说明,该经销店要获得最大月利润,售价应定为每吨多少元.
分析 (1)紧紧围绕“当每吨售价每下降10元时,月销售量就会增加5吨”列代数式就可以得出结论,
(2)由售价是x元,降价为(260-x),所以销售量是增加7.5×$\frac{260-x}{10}$吨,那么售出的金额是x[($\frac{260-x}{10}$×7.5)+45],根据利润=每件的利润×销售额,可以求出函数的解析式.
(3)由(2)的结论转化为顶点式就可以求出售价和利润的最大值.
解答 解:(1)由题意,得
45+7.5×$\frac{260-220}{10}$=75;
答:当每吨售价是220元时,此时的月销售量是75吨;
(2)由题意,得
y=(x-100)(45+$\frac{260-x}{10}$×7.5),
y=-$\frac{3}{4}$x2+315x-24000;
(3)∵y=-$\frac{3}{4}$x2+315x-24000;
∴y=-$\frac{3}{4}$(x-210)2+9075,
∴当x=210时,y最大=9075,
答:每吨材料售价定为210元时,该经销店获得的月利润最大.,
点评 本题考查了把实际问题转化为二次函数,再对二次函数进行实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
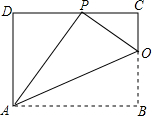 已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.
已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA. 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是25°.
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是25°.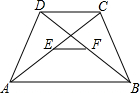 如图:AB∥CD,E,F分别是AC,DB的中点.
如图:AB∥CD,E,F分别是AC,DB的中点.