题目内容
2.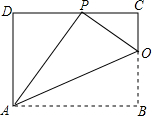 已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.
已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长.
分析 ①只需证明两对对应角分别相等即可证到两个三角形相似;
②根据相似三角形的性质求出PC长以及AP与OP的关系,然后在Rt△PCO中运用勾股定理求出OP长,从而求出AB长.
解答 解:①∵四边形ABCD是矩形,
∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.
由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B.
∴∠APO=90°.
∴∠APD=90°-∠CPO=∠POC.
∵∠D=∠C,∠APD=∠POC.
∴△OCP∽△PDA.
②∵△OCP与△PDA的面积比为1:4,
∴$\frac{OC}{PD}$=$\frac{OP}{PA}$=$\frac{CP}{DA}$=$\sqrt{\frac{1}{4}}$=$\frac{1}{2}$.
∴PD=2OC,PA=2OP,DA=2CP.
∵AD=8,
∴CP=4,BC=8.
设OP=x,则OB=x,CO=8-x.
在Rt△PCO中,
∵∠C=90°,CP=4,OP=x,CO=8-x,
∴x2=(8-x)2+42.
解得:x=5.
∴AB=AP=2OP=10.
∴边AB的长为10.
点评 此题考查了相似三角形的性质和判定,翻折的性质,矩形的性质勾股定理,掌握三角形相似的判定方法是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.一次函数y=kx+2k的图象可能是下列图象中的( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知在?ABCD中,对角线AC和BD相交于点O,AC=10,BD=8,AC与BD的夹角∠AOD=60°,求?ABCD的面积.
如图,已知在?ABCD中,对角线AC和BD相交于点O,AC=10,BD=8,AC与BD的夹角∠AOD=60°,求?ABCD的面积.