题目内容
8.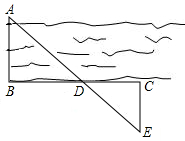 如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=150米,DC=60米,EC=50米,试求两岸间的距离AB.
如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=150米,DC=60米,EC=50米,试求两岸间的距离AB.
分析 先证明△ABD∽△ECD,然后利用相似比计算AB的长.
解答 解:∵AB⊥BC,CE⊥BC,
∴△ABD∽△ECD,
∴AB:CE=BD:CD,
即AB:50=150:60,
∴AB=125,
答:两岸间的距离AB=125米.
点评 本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,三点应在一条直线上.必须保证在一条直线上,为了使问题简便,尽量构造直角三角形.②测量方法:通过测量便于测量的线段,利用三角形相似,对应边成比例可求出河的宽度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.小明同学也发明了一个魔术盒,当任意有理数对(a,b)进入其中时,会得到一个新的有理数a2-b-1,例如把(3,-2)放入其中,就会得到32-(-2)-1=10,现将有理数对(-4,-2)放入其中,则会得到( )
| A. | 11 | B. | 17 | C. | 21 | D. | 23 |
3.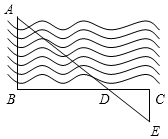 为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120m,DC=40m,EC=30m,那么这条河的大致宽度是( )
为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120m,DC=40m,EC=30m,那么这条河的大致宽度是( )
 为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120m,DC=40m,EC=30m,那么这条河的大致宽度是( )
为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得AB⊥BC,设BC与AE交于点D,如图所示测得BD=120m,DC=40m,EC=30m,那么这条河的大致宽度是( )| A. | 90m | B. | 60m | C. | 100m | D. | 120m |
17.下列说法正确的是( )
| A. | 有一组对角是直角的四边形一定是矩形 | |
| B. | 对角线互相平分的四边形是矩形 | |
| C. | 有一组邻角是直角的四边形一定是矩形 | |
| D. | 对角互补的平行四边形是矩形 |