题目内容
14. 如图,在平面直角坐标系中,一次函数y=k1x+2的图象与正比例函数y=k2x交于点A(m,1),点B是一次函数y=k1x+2的图象与x轴交点,且△AOB的面积为2.
如图,在平面直角坐标系中,一次函数y=k1x+2的图象与正比例函数y=k2x交于点A(m,1),点B是一次函数y=k1x+2的图象与x轴交点,且△AOB的面积为2.(1)求一次函数y=k1x+2的表达式及m的值;
(2)将正比例函数y=k2x的图象向上平移1个单位得到一个一次函数的图象,求这个一次函数的表达式.
分析 (1)过A作AC⊥BO,根据A点坐标可得AC=1,再根据△AOB的面积为2,可得BO=4,然后可得B点坐标,然后把B点坐标代入y=k1x+2可得k1的值,进而可得一次函数y=k1x+2的表达式,再把A点坐标代入y=k1x+2的表达式可得m的值;
(2)根据m的值可得A点坐标,然后再代入y=k2x可得解析式,再根据平移方法可得平移1个单位后所得一次函数解析式.
解答 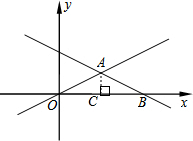 解:(1)过A作AC⊥BO,
解:(1)过A作AC⊥BO,
∵点A(m,1),
∴AC=1,
∵△AOB的面积为2,
∴BO=4,
∴B(4,0),
∵一次函数y=k1x+2的图象过B,
∴0=4k1+2,
解得:k1=-$\frac{1}{2}$,
∴一次函数解析式为y=-$\frac{1}{2}$x+2,
∵一次函数解析式为y=-$\frac{1}{2}$x+2过A,
∴1=-$\frac{1}{2}$m+2,
解得:m=2;
(2)∵m=2,
∴A(2,1),
∵y=k2x的图象过A,
∴1=2k2,
解得:k2=$\frac{1}{2}$,
∴y=k2x的解析式为y=$\frac{1}{2}$x,
∵正比例函数y=$\frac{1}{2}$x的图象向上平移1个单位得到一个一次函数的图象,
∴这个一次函数的表达式为y=$\frac{1}{2}$x+1.
点评 此题主要考查了求一次函数解析式,以及一次函数图象上点的坐标特点和几何变换,关键是掌握凡是函数图象经过的点必能满足解析式.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.下列各组线段中,能围成一个三角形的是( )
| A. | 1cm,2cm,3cm | B. | 2cm,3cm,4cm | C. | 3cm,6cm,3cm | D. | 3cm,8cm,5cm |
19.一元二次方程x2=9的根是( )
| A. | x1=x2=3 | B. | x1=x2=-3 | C. | x1=3,x2=-3 | D. | x1=x2=$\sqrt{3}$ |
 已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD°,交AB与H,∠AGE=50°,求∠BHF的度数.
已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD°,交AB与H,∠AGE=50°,求∠BHF的度数.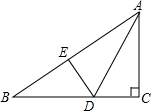 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,将∠C沿AD对折,使点C恰好落在AB边上的点E处,则BD的长度是2$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,将∠C沿AD对折,使点C恰好落在AB边上的点E处,则BD的长度是2$\sqrt{3}$.