题目内容
8.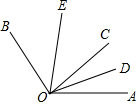 如图,∠AOB=120°,射线OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )
如图,∠AOB=120°,射线OC是∠AOB内部任意一条射线,OD,OE分别是∠AOC,∠BOC的角平分线,下列叙述正确的是( )| A. | ∠DOE的度数不能确定 | B. | ∠AOD=∠EOC | ||
| C. | ∠AOD+∠BOE=60° | D. | ∠BOE=2∠COD |
分析 根据角的平分线的定义以及角的和差即可判断.
解答 解:∵OD,OE分别是∠AOC,∠BOC的角平分线
∴∠COD=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}$∠BOC,
∴∠DOE=∠COD+∠EOC=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×120°=60°.
故C正确;
而OC是∠AOB内部任意一条射线,则∠BOC和∠AOC的大小无法确定,
则A、B、D错误.
故选C.
点评 本题考查了角的平分线的定义以及角的和差关系,正确理解∠DOE=$\frac{1}{2}$∠AOB是关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
19.在△ABC中,∠C=90°,下列选项中的关系式正确的是( )
| A. | sinA=$\frac{AC}{AB}$ | B. | cosB=$\frac{AC}{BC}$ | C. | tanA=$\frac{BC}{AB}$ | D. | AC=AB•cosA |
13.已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为( )
| A. | 6cm | B. | 9cm | C. | 3cm或6cm | D. | 1cm或9cm |
20. 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A. | ∠M=∠N | B. | AB=CD | C. | AM=CN | D. | AM∥CN |
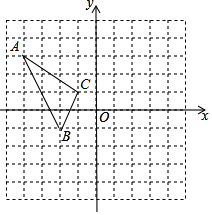 如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.
如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.