题目内容
19.若α、β为方程2x2-5x-1=0的两个实数根,则2α2+3αβ+5β的值为( )| A. | -13 | B. | 12 | C. | 14 | D. | 15 |
分析 根据一元二次方程解的定义得到2α2-5α-1=0,即2α2=5α+1,则2α2+3αβ+5β可表示为5(α+β)+3αβ+1,再根据根与系数的关系得到α+β=$\frac{5}{2}$,αβ=-$\frac{1}{2}$,然后利用整体代入的方法计算.
解答 解:∵α为2x2-5x-1=0的实数根,
∴2α2-5α-1=0,即2α2=5α+1,
∴2α2+3αβ+5β=5α+1+3αβ+5β=5(α+β)+3αβ+1,
∵α、β为方程2x2-5x-1=0的两个实数根,
∴α+β=$\frac{5}{2}$,αβ=-$\frac{1}{2}$,
∴2α2+3αβ+5β=5×$\frac{5}{2}$+3×(-$\frac{1}{2}$)+1=12.
故选B.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了一元二次方程解的定义.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
9.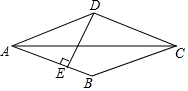 如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
 如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )
如图,菱形ABCD的周长为52,对角线AC的长为24,DE⊥AB,垂足为E,则DE的长为( )| A. | $\frac{75}{13}$ | B. | $\frac{96}{13}$ | C. | $\frac{120}{13}$ | D. | $\frac{144}{13}$ |
10.在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14. 如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )
如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )
 如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )
如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 50° |
11.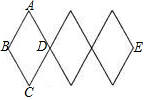 如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
 如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )| A. | (20$\sqrt{3}$-20)cm | B. | (40$\sqrt{3}$-40)cm | C. | (60-30$\sqrt{3}$)cm | D. | (60$\sqrt{3}$-60)cm |
 解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.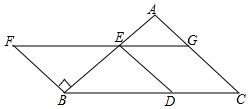 如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.