题目内容
20.先化简,再求值:$\frac{x-2}{{{x^2}+2x}}$÷$\frac{{{x^2}-4x+4}}{{{x^2}-4}}$-$\frac{1}{2x}$,其中x=$\sqrt{3}$.分析 先化简分式,然后将x的值代入即可求出答案.
解答 解:当x=$\sqrt{3}$时,
∴原式=$\frac{x-2}{x(x+2)}$÷$\frac{(x-2)^{2}}{(x+2)(x-2)}$-$\frac{1}{2x}$
=$\frac{x-2}{x(x+2)}$×$\frac{x+2}{x-2}$-$\frac{1}{2x}$
=$\frac{1}{x}$-$\frac{1}{2x}$
=$\frac{1}{2x}$
=$\frac{\sqrt{3}}{6}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
10.在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.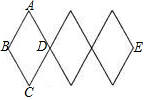 如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
 如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )| A. | (20$\sqrt{3}$-20)cm | B. | (40$\sqrt{3}$-40)cm | C. | (60-30$\sqrt{3}$)cm | D. | (60$\sqrt{3}$-60)cm |
15.小明和他的爸爸妈妈共3人站成一排拍照,他的爸爸妈妈相邻的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
5.化简:|-15|等于( )
| A. | 15 | B. | -15 | C. | ±15 | D. | $\frac{1}{15}$ |
4.下列各数中,无理数的是( )
| A. | 0 | B. | -1 | C. | $\sqrt{2}$ | D. | 1.414 |
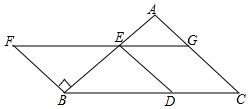 如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.