题目内容
7．
如图，一张圆心角为45°的扇形纸板剪得一个边长为1的正方形，则扇形纸板的面积是$\frac{5}{8}$πcm2（结果保留π）
分析 先求出扇形的半径，再根据面积公式求出面积．
解答 
解：如图1，连接OD，
∵四边形ABCD是边长为1的正方形，
∴∠DCB=∠ABO=90°，AB=BC=CD=1，
∵∠AOB=45°，
∴OB=AB=1，
由勾股定理得：OD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∴扇形的面积是$\frac{45•π×（\sqrt{5}）^{2}}{360}$=$\frac{5}{8}$π；
故答案是：$\frac{5}{8}$π．
点评 本题考查了正方形性质，勾股定理，扇形的面积公式的应用，解此题的关键是求出扇形的半径，题目比较好，难度适中．
练习册系列答案
相关题目
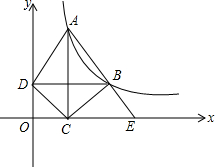如图，反比例函数y=$\frac{k}{x}$（x＞0，k≠0）的图象经过点A（1，6），过点A作AC⊥x轴于点C，点B在直线AC右侧的函数图象上，过点B作BD⊥y轴于点D，交AC于点F，连接BC、AD、CD．
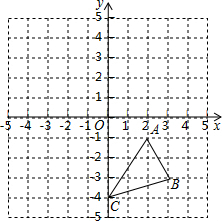在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，-1），B（3，-3），C（0，-4）
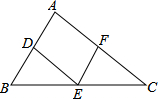如图，在△ABC中，点D、E、F分别是边AB、BC、CA上的中点，且AB=6cm，AC=8cm，则四边形ADEF的周长等于14cm．