题目内容
17. 如图,两个正方形的边长分别为a cm,b cm(a>b),若a+b=13,ab=35,求图中阴影部分的面积.
如图,两个正方形的边长分别为a cm,b cm(a>b),若a+b=13,ab=35,求图中阴影部分的面积.
分析 阴影部分面积=两个正方形面积减去两个直角三角形面积,整理后将a+b与ab的值代入计算即可求出值.
解答 解:根据题意得:S阴影部分=a2+b2-$\frac{1}{2}$a2-$\frac{1}{2}$b(a+b)=a2+b2-$\frac{1}{2}$a2-$\frac{1}{2}$ab-$\frac{1}{2}$b2=$\frac{1}{2}$(a2+b2+ab)=$\frac{1}{2}$[(a+b)2-ab]cm2,
把a+b=13,ab=35代入得:S阴影部分=67(cm2).
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
16.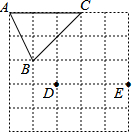 如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
 如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
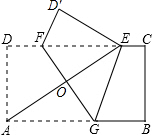 如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G、F、AE与FG交于点O.求证:A,G,E,F四点围成的四边形是菱形.
如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G、F、AE与FG交于点O.求证:A,G,E,F四点围成的四边形是菱形.