题目内容
1．三个连续自然数的和小于18，这样的自然数共有多少组？把它们写出来．分析 可设最小的数为x，表示出较大的两个数，让这3个数相加的结果小于18，解不等式，求自然数解的个数即可．
解答 解：设最小的数为x，则其余2个数为（x+1），（x+2），由题意得
x+（x+1）+（x+2）＜18，
解得：x＜5，
∵x是自然数，
∴x可取0、1、2、3、4共5个，
∴这样的数共有5组分别为（0，1，2）、（1，2，3）、（2，3，4）、（3，4，5）、（4、5、6）．
点评 考查一元一次不等式的应用，得到3个数的代数式是解决本题的突破点，易错点是求得最小数的自然数解．
练习册系列答案
教材全解字词句篇系列答案
相关题目
11．若y=$\frac{1}{\sqrt{4-x}}$有意义，则x的取值范围是（ ）
| A． | x≠4 | B． | x≤4 | C． | x≥4 | D． | x＜4 |
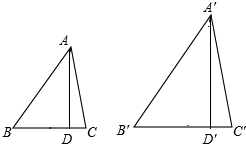如图所示，已知△ABC与△A′B′C′，AD⊥BC于D，A′D′⊥B′C′于D′，且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$，∠B=∠B′，试说明△ABC∽△A′B′C′．