Question

12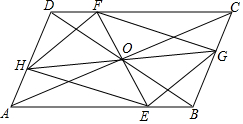．如图所示，过?ABCD的对角线交点O作直线EF，GH分别交各边于点E，F，G，H，依次连接E，G，F，H．求证：四边形EGFH是平行四边形．

Answer 1

分析 首先根据平行四边形的性质可得AO=CO，BO=DO，AD∥BC，再证明△AEO≌△CFO，进而得到EO=FO，进而得出GO=HO，可根据对角线互相平分的四边形是平行四边形进行判定

解答 证明：∵四边形ABCD是平行四边形，
∴AO=CO，BO=DO，AD∥BC，
∴∠EAO=∠FCO，
在△AEO和△CFO中，
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=CO}\\{∠AOE=∠FOC}\end{array}\right.$，
∴△AEO≌△CFO（AAS），
∴EO=FO，
同理可得：△BGO≌△DHO，
∴GO=HO，
∴四边形EGFH是平行四边形．

点评 此题主要考查了平行四边形的性质与判定，关键是掌握平行四边形对角线互相平分，对角线互相平分的四边形是平行四边形．