题目内容

分解因式：3x-3y-12（x-y）3．
考点：提公因式法与公式法的综合运用
专题：
分析：根据分组法，可得（3x-3y）-12（x-y）3，根据提取公因式，再套用公式，可得答案．
解答：解：原式=（3x-3y）-12（x-y）3
=3（x-y）-12（x-y）3
=3（x-y）[1-（x-y）2]
=3（x-y）（1+x-y）（1-x+y）．
点评：本题考查了因式分解，分组法，提公因式法分解因式，平方差公式，注意分解要彻底．
练习册系列答案
相关题目
求|x-5|+|x-2|的最小值．
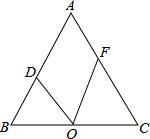如图，△ABC是等边三角形，O是BC中点．若∠DOF=60°，BD=3，CF=4，则△ABC的面积为（　　）
A、12
2
B、24
C、12
3
D、24
3
计算：
2
3x
-
9x
-x2
1
x3
+6x
x
16
．
通分：
x
3y
与
3x
2y2
．
多项式-36a2bc-48ab2c+24abc2的公因式是
 
．
观察数列：
1
3
，-
2
15
，
3
35
，-
4
63
…．则第五个数是
 
．
如图，在△ABC中，BC=4，AC=4，∠ACB=90°，F为AC中点，连接BF，过点C作CE⊥BF于O点，交AB于E点，连接EF．求证：
（1）∠AFE=∠BFC；
（2）EF+EC=BF．
已知线段AB=6，C是线段AB的中点，则线段AC长为（　　）
A、6B、3C、3或6D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网