题目内容
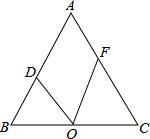如图，△ABC是等边三角形，O是BC中点．若∠DOF=60°，BD=3，CF=4，则△ABC的面积为（ ）A、12
| ||
| B、24 | ||
C、12
| ||
D、24
|
考点：相似三角形的判定与性质,等边三角形的性质
专题：
分析：由条件证明△BOD∽△CFO，可得到
=
，且BO=OC，代入可求得BO的长，进一步可得BC的长，利用等边三角形的面积求得△ABC的面积．
| BD |
| OC |
| BO |
| CF |
解答：解：∵△ABC为等边三角形，
∴∠B=∠C=60°，
∵∠DOF=60°，
∴∠DOB+∠FOC=∠DOB+∠BDO=120°，
∴∠BDO=∠FOC，
∴△△BOD∽△CFO，
∴
=
，
∵O是BC中点，
∴BO=CO，
∴BO2=3×4=12，
∴BO=2
，
∴BC=4
，
∴S△ABC=
•BC2=
×（4
）2=12
，
故选C．
∴∠B=∠C=60°，
∵∠DOF=60°，
∴∠DOB+∠FOC=∠DOB+∠BDO=120°，
∴∠BDO=∠FOC，
∴△△BOD∽△CFO，
∴
| BD |
| OC |
| BO |
| CF |
∵O是BC中点，
∴BO=CO，
∴BO2=3×4=12，
∴BO=2
| 3 |
∴BC=4
| 3 |
∴S△ABC=
| ||
| 4 |
| ||
| 4 |
| 3 |
| 3 |
故选C．
点评：本题主要考查相似三角形的判定和性质及等边三角形的性质，求出等边三角形的边长是解题的关键，注意公式S等边三角形=
a2（a为等边三角形的边长）的利用．
| ||
| 4 |
练习册系列答案
相关题目
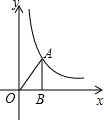如图，Rt△OAB在平面直角坐标系，直角顶点B在x轴的正半轴上，已知∠OBA=90°，OB=3，sin∠AOB=
要在燃气管道L上修建一个泵站C，分别向A，B两镇供气，泵站修在管道的什么地方，可使所用的输气管线到两地的距离一样？
一张5米长的梯子AB靠在墙上，梯子的底部B离墙角C有3米，如果梯子的顶部A下滑1米，问梯子的底部B向外滑出多少米？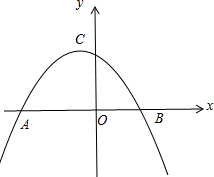
如图，抛物线y=-
在等边△ABC中，CD是高线，求sinA，cosA，sin∠ACD，cos∠ACD．