题目内容
16．
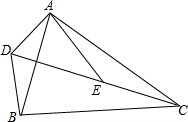已知$\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$，求证：△ADB∽△AEC．
分析 利用相似三角形的判定方法得出△ADE∽△ABC，再利用相似三角形的性质得出∠DAE=∠BAC，进而再利用相似三角形的判定得出答案．
解答 证明：∵$\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$，
∴△ADE∽△ABC，
∴∠DAE=∠BAC，
∴∠DAB=∠EAC，
又∵$\frac{AD}{AB}$=$\frac{AE}{AC}$，
∴△ADB∽△AEC．
点评 此题主要考查了相似三角形的判定与性质，得出∠DAB=∠EAC是解题关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
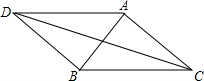等腰Rt△ABC中，AB=AC，∠BAC=90°，点D在△ABC外，且∠ADB=45°，BD=3，AD=4，求线段DC的长．
如图，AB是⊙O的直径，点C在⊙O上，OD⊥BC，交BC于D，若BD=1，则BC的长为2．