题目内容
15. 如图,在△ABC中,∠A=70°,AC=BC,以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′BC′,点A′恰好落在AC上,连接CC′,则∠ACC′=110°.
如图,在△ABC中,∠A=70°,AC=BC,以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′BC′,点A′恰好落在AC上,连接CC′,则∠ACC′=110°.
分析 由∠A=70°,AC=BC,可知∠ACB=40°,根据旋转的性质,AB=BA′,BC=BC′,∠CBC′=∠α=40°,∠BCC′=70°,于是∠ACC′=∠ACB+∠BCC′=110°.
解答 解:∵∠A=70°,AC=BC,
∴∠BCA=40°,
根据旋转的性质,AB=BA′,BC=BC′,
∴∠α=180°-2×70°=40°,
∵∠∠CBC′=∠α=40°,
∴∠BCC′=70°,
∴∠ACC′=∠ACB+∠BCC′=110°;
故答案为:110°.
点评 本题主要考查了旋转的性质、等腰三角形的性质,熟练掌握旋转前后的图形对应边相等、旋转角相等是解决问题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
6.|-$\frac{1}{2}$|的相反数是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
3.“五一”期间,某校团委组织500团员前往烈士陵园,开展“缅怀革命先烈,立志为国成才”的活动.由甲、乙两家旅行社来承担此次活动的出行事宜.由于接待能力有限,两家旅行社每家做多只能接待300人.甲旅行社的费用是每人4元,乙旅行社的费用是每人6元.如果设甲旅行社安排x人,乙旅行社安排y人,所需总费用为w元,则:
(1)试求w与x的函数关系,并求当x为何值时出行费用w最低?
(2)经协商,两家旅行社均同意对写生施行优惠政策,其优惠政策如表:
如何安排人数,可使出行费用最低?
(1)试求w与x的函数关系,并求当x为何值时出行费用w最低?
(2)经协商,两家旅行社均同意对写生施行优惠政策,其优惠政策如表:
| 人数 | 甲旅行社 | 乙旅行社 |
| 少于250人 | 一律八折优惠 | 七折优惠 |
| 不少于250人 | 五折优惠 |
20.一个正方体的体积为25,估计这个正方形的边长在( )
| A. | 2和3之间 | B. | 3和4之间 | C. | 4和5之间 | D. | 5和6之间 |
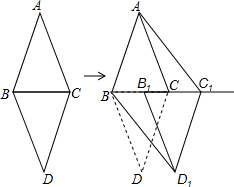 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为7cm.
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为7cm.