题目内容
19.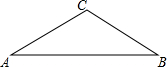 如图,已知在等腰△ABC中,∠C=120°
如图,已知在等腰△ABC中,∠C=120°(1)尺规作图:①过点C作CD⊥AC交AB于点D.
②过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线.
分析 (1)利用过直线上一点作直线的垂线确定D点,再作AD的垂直平分线确定AD的中点O,然后以点O为圆心,OA为半径作⊙O即可;
(2)连结OC,根据圆周角定理,由∠ACD=90°可判断AD是⊙O的直径,再利用等腰三角形的性质和三角形内角和求出∠A=∠B=30°,接着由OA=OC得∠ACO=∠A=30°,所以∠BCO=∠ACB-∠ACO=90°,根据切线的判定定理得到BC是⊙O的切线.
解答 (1)解:如图;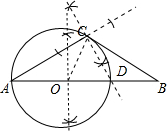
(2)证明:连结OC,
∵CD⊥AC,
∴∠ACD=90°,
∴AD是⊙O的直径,
∵CA=CB,∠C=120°
∵∠A=∠B=30°,
又∵OA=OC,
∴∠ACO=∠A=30°,
∴∠BCO=∠ACB-∠ACO=120°-30°=90°,
∴BC⊥OC,
∴BC是⊙O的切线.
点评 本题考查了复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了等腰三角形的性质和切线的判定定理.

练习册系列答案
相关题目
14.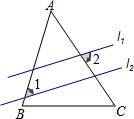 如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )
 如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )| A. | 45° | B. | 55° | C. | 80° | D. | 100° |
 小华和小军玩纸牌游戏.如图是同一副扑克中的4张扑克牌的正面,将它们正面朝下洗匀后放在桌上,小华先从中抽出一张,小军从剩余的3张牌中再抽出一张.
小华和小军玩纸牌游戏.如图是同一副扑克中的4张扑克牌的正面,将它们正面朝下洗匀后放在桌上,小华先从中抽出一张,小军从剩余的3张牌中再抽出一张.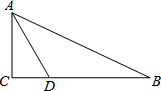 在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,则BC的长是3.
在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,则BC的长是3.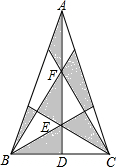 如图,在等腰三角形中,AB=AC,BC=4,D为BC的中点,点E、F在线段AD上,tan∠ABC=3,则阴影部分的面积是6.
如图,在等腰三角形中,AB=AC,BC=4,D为BC的中点,点E、F在线段AD上,tan∠ABC=3,则阴影部分的面积是6.