题目内容
9.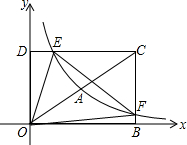 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0),若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0),若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请直接写出不等式k2x+b-$\frac{{k}_{1}}{x}$<0的解集.
分析 (1)由点B、D的坐标结合矩形的性质即可得出点C的坐标,由中点的性质即可得出点A的坐标,再结合反比例函数图象上点的坐标特征即可得出k值,由此即可得出反比例函数解析式;由点F的横坐标、点E的纵坐标结合反比例函数解析式即可得出点E、F的坐标,再由点E、F的坐标利用待定系数法即可求出直线EF的解析式;
(2)通过分割图形并利用三角形的面积公式即可求出结论;
(3)观察函数图象,根据两函数图象的上下关系结合交点坐标即可得出不等式的解集.
解答 解:(1)∵D(0,4),B(6,0),
∴C(6,4),
∵点A为线段OC的中点,
∴A(3,2),
把A(3,2)代入y=$\frac{{k}_{1}}{x}$(x>0),得:k1=6,
∴反比例函数为y=$\frac{6}{x}$,
把x=6代入y=$\frac{6}{x}$得y=1,则F点的坐标为(6,1);
把y=4代入y=$\frac{6}{x}$得4=$\frac{6}{x}$,解得:x=$\frac{3}{2}$,则E点的坐标为($\frac{3}{2}$,4).
把F(6,1)、E($\frac{3}{2}$,4)代入y=k2x+b中得:$\left\{\begin{array}{l}{\frac{3}{2}{k}_{2}+b=4}\\{6{k}_{2}+b=1}\end{array}\right.$得:k2=-$\frac{2}{3}$,b=5,
∴直线EF的解析式为y=-$\frac{2}{3}$x+5;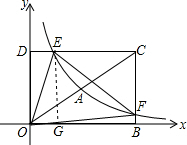
(2)过点E作EG⊥OB于点G
∵点E、F都在反比例函数图象上
∴S△EOG=S△OBF,
∴S△EOF=S梯形EFBG,
∵E($\frac{3}{2}$,4),F(6,1),
∴EG=4,FB=1,BG=$\frac{9}{2}$,
∴S△EOF=S梯形EFBG=$\frac{1}{2}$(1+4)×$\frac{9}{2}$=$\frac{45}{4}$;
(3)不等式k2x+b-$\frac{{k}_{1}}{x}$<0,可变形为-$\frac{2}{3}$x+5<$\frac{6}{x}$.
观察函数图象可发现:
当0<x<$\frac{3}{2}$或x>6时,一次函数y=-$\frac{2}{3}$x+5的图象在反比例函数y=$\frac{6}{x}$的图象的下方,
∴-$\frac{2}{3}$x+5-$\frac{6}{x}$<0的解集为:0<x<$\frac{3}{2}$或x>6.
点评 本题考查了矩形的性质、反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征、待定系数法求函数解析式以及三角形的面积公式,本题属于基础题,难度不大,解决该题型题目时,求出点的坐标,再结合点的坐标利用待定系数法求出函数解析式是关键.

| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
| A. | 正三角形 | B. | 正方形 | C. | 正六边形 | D. | 正十边形 |
| A. |  | B. |  | C. |  | D. |  |
| A. | 0.25×10-2 | B. | 2.5×10-3 | C. | 2.5×10-2 | D. | 2.5×104 |
| A. | 2m+3n=5mn | B. | a6÷a2=a4 | C. | (a2)3=a6 | D. | a•a2=a3 |
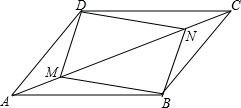 如图,在?ABCD中,AM=CN,求证:四边形DMBN为平行四边形.
如图,在?ABCD中,AM=CN,求证:四边形DMBN为平行四边形.