Question

1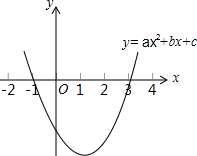．二次函数y=ax²+bx+c（a≠0）的图象如图所示，下列说法：
①2a+b=0
②当-1≤x≤3时，y＜0
③若（x₁，y₁）、（x₂，y₂）在函数图象上，当x₁＜x₂时，y₁＜y₂ 
④9a+3b+c=0
其中正确的有（填写正确的序号）①④．

Answer 1

分析 根据抛物线对称轴可判断①；根据图象知当-1≤x≤3时图象位于x轴下方或在x轴上，可判断②；根据函数对称轴即可判断增减性，可判断③；由图象过（3，0）可判断④．

解答 解：由图象可知，当x=-1时，y=0；当x=3时，y=0；
∴抛物线解析式为x=1，即-$\frac{b}{2a}$=1，得：2a+b=0，故①正确；
当-1≤x≤3时，y≤0，故②错误；
当x₁＜x₂＜1时，y₁＞y₂，故③错误；
∵抛物线过（3，0），
∴将（3，0）代入得：9a+3b+c=0，故④正确；
故答案为：①④．

点评 本题考查了二次函数图象与系数的关系，解题的关键是结合图象逐条分析．解决该题型题目时，结合图象上的点找出二次函数各系数间的关系是关键．