题目内容
20.已知抛物线y=x2+bx+c,经过点A(0,5)和点B(3,2).(1)求抛物线的解析式;
(2)指出它的开口方向,对称轴和顶点坐标.
(3)若A(m,y)B(m+1,y)都在函数图象上,比较y与y的大小.
分析 (1)把点A、B的坐标代入函数解析式,根据待定系数法列式求解即可.
(2)配成顶点式,再根据二次函数的性质求解.
(3)根据函数的增减性进行解答即可.
解答 解:(1)∵抛物线y=x2+bx+c经过点A(0,5)和B(3,2)点,
∴$\left\{\begin{array}{l}{c=5}\\{9+3b+c=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-4}\\{c=5}\end{array}\right.$,
∴抛物线的解析式是:y=x2-4x+5.
(2)y=x2-4x+5=(x-2)2+1,
∵a=1>0,
∴抛物线开口向上,
对称轴为直线x=2,顶点坐标为(2,1).
(3)∵A(m,y1)比B(m+1,y2)离对称轴x=2近,
∴y1<y2.
点评 主要考查了用待定系数法求二次函数的解析式、二函数的性质,是基础题,熟练掌握待定系数法是解题的关键.

练习册系列答案
相关题目
11.方程组$\left\{\begin{array}{l}{x-y=k+2}\\{x+3y=k}\end{array}\right.$的解适合方程x+y=2,则k值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -$\frac{1}{2}$ |
8.已知一组数,3,5,9,17…,用代数式表示第n个数为( )
| A. | 3+2n | B. | n2+1 | C. | 2n+1 | D. | 不能确定 |
5.在$-\frac{1}{2}$,$-\frac{1}{3}$,0,$\frac{1}{2}$中,最小的是( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{3}$ | C. | 0 | D. | $\frac{1}{2}$ |
10.在平面直角坐标系内点P(-3,a)与点Q(b,-1)关于y轴对称,则a+b的值为( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |

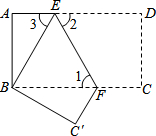 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.