题目内容
15.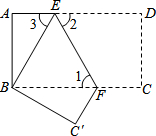 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.(1)折叠后,DC的对应线段是BC′,CF的对应线段是FC′;
(2)若AB=8,DE=10,求CF的长度.
分析 (1)根据翻折后的对应点确定出对应线段即可;
(2)在Rt△ABE中由勾股定理可求得AE=6,从而得到AD=16,然后证明BE=BF=10,从而可求得FC=16-10=6.
解答 解:(1)∵点D与点B重合,点C落在点C′的位置上,
∴DC的对应线段是BC′,CF的对应线段是FC′.
故答案为:BC′;FC′.
(2)由翻折的性质可知:DE=BE=10,∠2=∠BEF.
∵AD∥BC,
∴∠2=∠1.
∴∠1=∠BEF.
∴BE=BF=10.
在Rt△ABE中,由勾股定理得:AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴AD=AE+ED=6+10=16.
∴CF=CB-BF=16-10=6.
点评 本题主要考查的是翻折的性质、勾股定理的应用,证得BE=BF=10是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列说法正确的是( )
| A. | 单项式y的次数是1,系数是0 | B. | 多项式$\frac{3(1-{x}^{2})}{8}$中x2的系数是-$\frac{3}{8}$ | ||
| C. | 多项式t-5的项是t和5 | D. | $\frac{xy-1}{2}$是二次单项式 |
4.如图①是4×4正方形方格,已有两个正方形方格被涂黑,请你再将其中两个方格涂黑,并且使得涂黑后的整个图案是轴对称图形,约定经过旋转后全等的图案都视为同一种,图②中的两幅图就视为同一种,则得到的不同图案共有( )
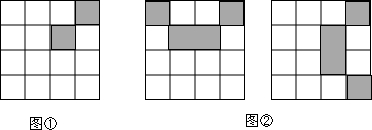

| A. | 6种 | B. | 7种 | C. | 8种 | D. | 9种 |
5.根据下列表格的对应值:判断方程ax2+bx+c=0一个解的取值范围是( )
| x | 0.59 | 0.60 | 0.61 | 0.62 | 0.63 |
| ax2+bx+c | -0.0619 | -0.04 | -0.0179 | 0.0044 | 0.0269 |
| A. | 0.59<x<0.61 | B. | 0.60<x<0.61 | C. | 0.61<x<0.62 | D. | 0.62<x<0.63 |
 如图,在平面直角坐标系xOy中,二次函数y=ax2+bx的顶点为D(1,-1),且与x轴交于O,A两点,二次函数y=ax2+bx的图象记作G1,把G1向右平移m(m>0)个单位得到的图象记作G2,G2与x轴交于B,C两点,且G2与G1相交于点P.
如图,在平面直角坐标系xOy中,二次函数y=ax2+bx的顶点为D(1,-1),且与x轴交于O,A两点,二次函数y=ax2+bx的图象记作G1,把G1向右平移m(m>0)个单位得到的图象记作G2,G2与x轴交于B,C两点,且G2与G1相交于点P.