题目内容
6. 如图,从位于六和塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°.若此观测点离地面的高度CD为30米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,则A,B之间的距离为( )米.
如图,从位于六和塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°.若此观测点离地面的高度CD为30米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,则A,B之间的距离为( )米.| A. | 30+10$\sqrt{3}$ | B. | 40$\sqrt{3}$ | C. | 45 | D. | 30+15$\sqrt{3}$ |
分析 在Rt△ACD和Rt△CDB中分别求出AD,BD的长度,然后根据AB=AD+BD即可求出AB的值.
解答 解:由题意得,∠ECA=45°,∠FCB=60°,
∵EF∥AB,
∴∠CAD=∠ECA=45°,∠CBD=∠FCB=60°,
∵∠ACD=∠CAD=45°,
在Rt△CDB中,tan∠CBD=$\frac{CD}{BD}$,
∴BD=$\frac{30}{tan60°}$=10$\sqrt{3}$米,
∵AD=CD=30米,
∴AB=AD+BD=30+10$\sqrt{3}$米,
故选A.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形,并利用解直角三角形的知识解直角的三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )
一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )
 一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )
一个正方体的表面展开图如图所示,则原正方体中“行”字所在的面相对的面上标的字是( )| A. | 步 | B. | 量 | C. | 青 | D. | 春 |
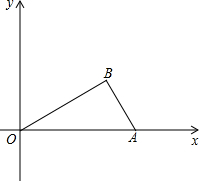 如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(t>0且t≠4):
如图,在平面直角坐标系中,Rt△ABO的斜边OA在x轴上,点B在第一象限内,AO=4,∠BOA=30°.点C(t,0)是x轴正半轴上一动点(t>0且t≠4):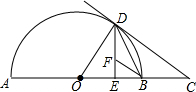 如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD.
如图,AB是半圆O的直径,过半圆O上一点D作DE⊥AB,垂足为E,作半圆O的切线DC,交AB的延长线于点C,连结OD、BD. 如图,直线a∥b,∠1=50°,∠2=30°,则∠3=20°.
如图,直线a∥b,∠1=50°,∠2=30°,则∠3=20°.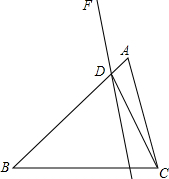 如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.
如图,已知△ABC,D为AB边上一点,∠BDC=∠ACB,过点D作直线DF.