��Ŀ����
11��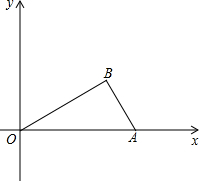 ��ͼ����ƽ��ֱ������ϵ�У�Rt��ABO��б��OA��x���ϣ���B�ڵ�һ�����ڣ�AO=4����BOA=30�㣮��C��t��0����x����������һ���㣨t��0��t��4����
��ͼ����ƽ��ֱ������ϵ�У�Rt��ABO��б��OA��x���ϣ���B�ڵ�һ�����ڣ�AO=4����BOA=30�㣮��C��t��0����x����������һ���㣨t��0��t��4������1����B������Ϊ��3��$\sqrt{3}$��������O��B��A�������߽���ʽΪy=-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x��
��2������OBC�����Բ��P����Բ��P�ڣ�1������������ʱ�����C��Բ��P�����ꣻ
��3�����OBC�����Բ��P��y�����һ����ΪD���뽫OD�ú�t�Ĵ���ʽ��ʾ����������CD����Сֵ��
���� ��1����BE��OA��E�����BEO=90�㣬�������Ǻ������OB���������Ǻ������BE��OE�����ɵó���B�����ꣻ�ô���ϵ������������ߵĽ���ʽ���ɣ�
��2�������OB���д��ߵĽ���ʽ���ó�P��$\frac{t}{2}$��-$\frac{\sqrt{3}}{2}t$+2$\sqrt{3}$�����ѵ�P������������߽���ʽ���ⷽ�����t�����ɵó�P��C�����ꣻ
��3������CD����CDΪֱ�����ó���DBC=90�㣻�����������
�ٵ���C���߶�OA��ʱ��֤����ABC�ס�OBD���ó�����ʽ$\frac{OD}{AC}=\frac{OB}{AB}$�����ɵó�OD�����ݹ��ɶ����������CD����Сֵ��
�ڵ���C�ڵ�A�ұߣ�t��4��ʱ��ͬ���ɵã���ABC�ס�OBD���ó�OD=$\sqrt{3}$t-4$\sqrt{3}$�����ݹ��ɶ������ɵó�CD����Сֵ��
��� �⣺��1����BE��OA��E����ͼ1��ʾ��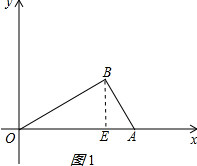
���BEO=90�㣬
�ߡ�ABO=90�㣬��BOA=30�㣬
��OB=OA•cos30��=4��$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$��
��BE=$\frac{1}{2}$OB=$\sqrt{3}$��
��OE=$\sqrt{3}$BE=3��
���B����������3��$\sqrt{3}$����
�ʴ�Ϊ����3��$\sqrt{3}$����
��O��0��0����A��4��0����B��3��$\sqrt{3}$����
�����O��B��A�������߽���ʽΪy=ax2+bx��
��������ã�$\left\{\begin{array}{l}{16a+4b=0}&{\;}\\{9a+3b=\sqrt{3}}&{\;}\end{array}\right.$��
��ã�a=-$\frac{\sqrt{3}}{3}$��b=$\frac{4\sqrt{3}}{3}$��
�����O��B��A�������߽���ʽΪ��y=-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x��
�ʴ�Ϊ��y=-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x��
��2����ͼ2��ʾ��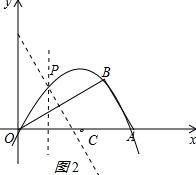 �����ԲԲ��P��ֱ��x=$\frac{t}{2}$��OB���д��߽��㣬
�����ԲԲ��P��ֱ��x=$\frac{t}{2}$��OB���д��߽��㣬
���P�ĺ�����Ϊ$\frac{t}{2}$��
��OB���д��߹��㣨2��0����OB���е㣨$\frac{3}{2}$��$\frac{\sqrt{3}}{2}$����
��OB���д��ߵĽ���ʽΪ��y=kx+b��
��$\left\{\begin{array}{l}{2k+b=0}\\{\frac{3}{2}k+b=\frac{\sqrt{3}}{2}}\end{array}\right.$��
���k=-$\sqrt{3}$��b=2$\sqrt{3}$��
��OB���д��ߵĽ���ʽΪ��y=-$\sqrt{3}$x+2$\sqrt{3}$��
��P��$\frac{t}{2}$��-$\frac{\sqrt{3}}{2}t$+2$\sqrt{3}$����
ҪʹP���������ϣ���P����������$\frac{\sqrt{3}}{2}$t+2$\sqrt{3}$=-$\frac{\sqrt{3}}{3}$����$\frac{t}{2}$��2+$\frac{4\sqrt{3}}{3}$��$\frac{t}{2}$��
��ã�t=2����t=12��
��P���������1��$\sqrt{3}$������6��-4$\sqrt{3}$����
��C��������2��0������12��0����
��3������CD��BD����ͼ3��ʾ��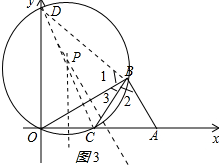 ��CDΪֱ����
��CDΪֱ����
���DBC=90�㣻
������������ٵ���C���߶�OA��ʱ��
�ߡ�DBC=��OBA=90�㣬
���1+��3=��2+��3=90�㣬
����1=��2��
�֡ߡ�BOD=��BAC=60�㣬
���ABC�ס�OBD��
��$\frac{OD}{AC}=\frac{OB}{AB}$��
��OD=$\frac{��4-t����2\sqrt{3}}{2}$=-$\sqrt{3}$t+4$\sqrt{3}$��
���ݹ��ɶ����ã�CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=$\sqrt{��-\sqrt{3}t+4\sqrt{3}��^{2}+{t}^{2}}$=$\sqrt{4��t-3��^{2}+12}$��
�൱t=3ʱ��CD����СֵΪ2$\sqrt{3}$��
�ڵ���C�ڵ�A�ұߣ�t��4��ʱ��
ͬ���ɵã���ABC�ס�OBD��
��OD=$\sqrt{3}$t-4$\sqrt{3}$��
���ݹ��ɶ����ã�CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=$\sqrt{��\sqrt{3}t-4\sqrt{3}��^{2}+{t}^{2}}$=$\sqrt{4��t-3��^{2}+12}$��
�൱t=3ʱ��CD����СֵΪ2$\sqrt{3}$��
����������ODΪ-$\sqrt{3}$t+4$\sqrt{3}$����$\sqrt{3}$t-4$\sqrt{3}$��CD����СֵΪ2$\sqrt{3}$��
���� ������Բ���ۺ���Ŀ��������������ͼ�����ʡ����Ǻ������ô���ϵ������һ�κ����Ͷ��κ����Ľ���ʽ��Բ�ܽǶ��������ɶ��������������ε��ж������ʡ���Сֵ��֪ʶ�������ѶȽϴ��ۺ���ǿ���ر��ǣ�2����3���У���Ҫͨ����������֤�����������ƺ����ֱ�ߵĽ���ʽ���ܵó������

| A�� | a2+a=2a3 | B�� | a3•a2=a6 | C�� | 2a6��a2=2a3 | D�� | ��a2��4=a8 |
| A�� | 0��d��4 | B�� | d��10 | C�� | 0��d��4��d��10 | D�� | 4��d��10 |
| A�� | 16��15 | B�� | 16��15.5 | C�� | 16��16 | D�� | 15.5��15.5 |
 ��ͼ����λ���������Ĺ۲��C�����������ײ�A��B�ĸ��Ƿֱ�Ϊ45���60�㣮���˹۲�������ĸ߶�CDΪ30�ף�A��B������CD�����࣬�ҵ�A��D��B��ͬһˮƽֱ���ϣ���A��B֮��ľ���Ϊ���������ף�
��ͼ����λ���������Ĺ۲��C�����������ײ�A��B�ĸ��Ƿֱ�Ϊ45���60�㣮���˹۲�������ĸ߶�CDΪ30�ף�A��B������CD�����࣬�ҵ�A��D��B��ͬһˮƽֱ���ϣ���A��B֮��ľ���Ϊ���������ף�| A�� | 30+10$\sqrt{3}$ | B�� | 40$\sqrt{3}$ | C�� | 45 | D�� | 30+15$\sqrt{3}$ |
 ��ͼ��A��C�ֱ���x�ᡢy���ϵĵ㣬˫����y=$\frac{2}{x}$��x��0�������OABC�ı�BC��AB�ֱ���E��F����AF��BF=1��2�����OEF�����Ϊ��������
��ͼ��A��C�ֱ���x�ᡢy���ϵĵ㣬˫����y=$\frac{2}{x}$��x��0�������OABC�ı�BC��AB�ֱ���E��F����AF��BF=1��2�����OEF�����Ϊ��������| A�� | 2 | B�� | $\frac{8}{3}$ | C�� | 3 | D�� | $\frac{10}{3}$ |
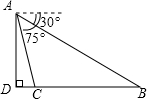 ��ͼ���Ӱ���ɽɽ��A������ǰ���ij�������B��C�ĸ��Ƿֱ�Ϊ30�㣬75�㣬����ɽ�ĸ߶�AD��600m�����Ŀ���BC���ڣ�������
��ͼ���Ӱ���ɽɽ��A������ǰ���ij�������B��C�ĸ��Ƿֱ�Ϊ30�㣬75�㣬����ɽ�ĸ߶�AD��600m�����Ŀ���BC���ڣ�������| A�� | 300��$\sqrt{3}$+1��m | B�� | 1200��$\sqrt{3}$-1��m | C�� | 1800��$\sqrt{3}$-1��m | D�� | 2400��$\sqrt{2}$-1��m |
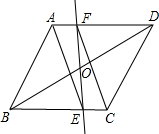 ��ͼ����?ABCD�У�O�ǶԽ���BD���е㣬��O���һ��ֱ�߷ֱ���BC�ཻ��E����AD�ཻ��F����֤���ı���AECF��ƽ���ı��Σ�
��ͼ����?ABCD�У�O�ǶԽ���BD���е㣬��O���һ��ֱ�߷ֱ���BC�ཻ��E����AD�ཻ��F����֤���ı���AECF��ƽ���ı��Σ�