题目内容
16.在平面直角坐标系中,一次函数的解析式为y=-$\frac{\sqrt{3}}{3}$x+2,与x轴交于B点,与y轴交于A点,若点Q在直线AB上,点P是坐标系中一点.(1)画出图形,并求∠ABO的度数;
(2)当△OBQ为等腰三角形时,求点Q的坐标;
(3)当以O、B、Q、P为顶点的四边形是菱形时,直接写出点P的坐标.
分析 (1)求出A、B两点坐标,可得OA、OB的长,可得tan∠ABO=$\frac{OA}{OB}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,由此即可解决问题;
(2)分三种情形讨论①O为等腰三角形的顶点.②B为等腰三角形的顶点.③Q为等腰三角形的顶点;
(3)分两种情形讨论①当OB为菱形的对角线时,易知P2($\sqrt{3}$,-1).②当OB为菱形的边时,根据平移的性质解决问题即可;
解答 解:(1)一次函数的解析式为y=-$\frac{\sqrt{3}}{3}$x+2的图象如图1所示,
∵一次函数y=-$\frac{\sqrt{3}}{3}$x+2,与x轴交于B点,与y轴交于A点,
∴A(0,2),B(2$\sqrt{3}$,0),
∴tan∠ABO=$\frac{OA}{OB}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠ABO=30°.
(2)如图2中,
①当OQ=BQ时,点Q的横坐标为$\sqrt{3}$,
x=$\sqrt{3}$时,y=-$\frac{\sqrt{3}}{3}$•$\sqrt{3}$+2=1,
可得Q1($\sqrt{3}$,1),
②OB=OQ时,OB=OQ2=2$\sqrt{3}$,∠OBQ2=∠OQ2B=30°,
易知Q2(-$\sqrt{3}$,3).
③当BQ=OB时,可得Q3(2$\sqrt{3}$-3,$\sqrt{3}$),Q4(2$\sqrt{3}$+3,-$\sqrt{3}$),
综上所述,满足条件的点Q的坐标为($\sqrt{3}$,1)或(-$\sqrt{3}$,3)或(2$\sqrt{3}$-3,$\sqrt{3}$),Q4(2$\sqrt{3}$+3,-$\sqrt{3}$).
(3)如图3中,
①当OB为菱形的对角线时,易知P2($\sqrt{3}$,-1).
②当OB为菱形的边时,由(2)可得Q1(2$\sqrt{3}$-3,$\sqrt{3}$),Q3(2$\sqrt{3}$+3,-$\sqrt{3}$),
向左平移2$\sqrt{3}$分别得到P1(-3,$\sqrt{3}$),P3(3,-$\sqrt{3}$),
综上所述,满足条件的点P坐标为($\sqrt{3}$,-1)或(-3,$\sqrt{3}$)或(3,-$\sqrt{3}$).
点评 本题考查一次函数综合题、等腰三角形的判定和性质、菱形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.


 如图所示的⊙O中,若∠DBC=∠BAC=30°,则∠BDO=30°.
如图所示的⊙O中,若∠DBC=∠BAC=30°,则∠BDO=30°.
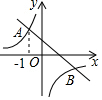 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$图象与一次函数y=kx+b的图象的2个交点分别为A(-1,n),B(2,n-3)
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$图象与一次函数y=kx+b的图象的2个交点分别为A(-1,n),B(2,n-3)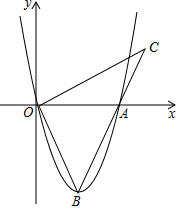 如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C.
如图,抛物线y=ax2-4x的图象与x轴的一个交点为A(6,0),点B为抛物线的顶点,连结OB、AB,作OC⊥OB交BA的延长线于点C.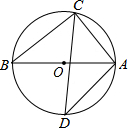 如图,已知AB是⊙O的直径,∠D=42°,则∠CAB的度数为48°.
如图,已知AB是⊙O的直径,∠D=42°,则∠CAB的度数为48°.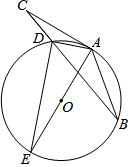 如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.
如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.