题目内容
6．某校积极开展“阳光体育”活动，共开设了跳绳、足球、篮球、跑步四种运动项目，为了解学生最喜爱哪一种项目，随机抽取了部分学生进行调查，并绘制了如下的条形统计图和扇形统计图（部分信息未给出）．
（1）求本次被调查的学生人数；
（2）补全条形统计图；
（3）该校共有1600名学生，请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少？
分析 （1）用喜欢跳绳的人数除以其所占的百分比即可求得被调查的总人数；
（2）用总人数乘以足球所占的百分比即可求得喜欢足球的人数，用总数减去其他各小组的人数即可求得喜欢跑步的人数，从而补全条形统计图；
（3）用样本估计总体即可确定最喜爱篮球的人数比最喜爱足球的人数多多少．
解答 解：（1）根据题意得：
10÷25%=40（人）；
答：本次被调查的学生人数是40人；
（2）喜欢足球的有40×30%=12人，
喜欢跑步的有40-10-15-12=3人，
补图如下：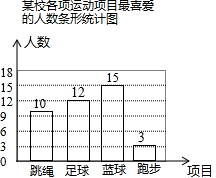
（3）全校最喜爱篮球的人数比最喜爱足球的人数多1600×$\frac{15-12}{40}$=120人．
点评 本题考查了扇形统计图、条形统计图及用样本估计总体的知识，读懂统计图，从统计图中得到必要的信息是解决问题的关键．
练习册系列答案
相关题目
14．
如图，在墙上固定一根木条，至少要固定两个点，能解释这一实际应用的数学知识是（ ）
如图，在墙上固定一根木条，至少要固定两个点，能解释这一实际应用的数学知识是（ ）| A． | 两点确定一条直线 | B． | 两点之间，线段最短 | ||
| C． | 直线上有无数个点 | D． | 点动成线 |
已知函数y=ax+b与y=cx+d的图象如图所示，则关于x的不等式ax+b≥cx+d的解集是x≥2．
11．
如图，点A是正方体小木块（质地均匀）的一个顶点，将木块随机投掷在水平桌面上，则稳定后点A与桌面接触的概率是（ ）
如图，点A是正方体小木块（质地均匀）的一个顶点，将木块随机投掷在水平桌面上，则稳定后点A与桌面接触的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{5}$ |
甲已经乘缆车到达山腰的位置，乙还在山脚．现在两人同时登山，他们距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：