题目内容
5. 在平面直角坐标系xOy中,一次函数的图象经过点A(4,1)与点B(0,5).
在平面直角坐标系xOy中,一次函数的图象经过点A(4,1)与点B(0,5).(1)求一次函数的表达式;
(2)若P点为此一次函数图象上一点,且S△POB=$\frac{3}{2}$S△AOB,求P点的坐标.
分析 (1)待定系数法求解可得;
(2)设P(x,-x+5),根据S△POB=$\frac{3}{2}$S△AOB可得$\frac{1}{2}$×OB•|xP|=$\frac{1}{2}$×OB•xA,即$\frac{1}{2}$×5•|xP|=$\frac{3}{2}$×$\frac{1}{2}$×5×4,解之求得xP即可知答案.
解答 解:(1)设一次函数的解析式为y=kx+b,
将A(4,1)、B(0,5)代入得:$\left\{\begin{array}{l}{4k+b=1}\\{b=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
∴一次函数表达式为y=-x+5;
(2)设P(x,-x+5),
∵S△POB=$\frac{3}{2}$S△AOB,
∴$\frac{1}{2}$×OB•|xP|=$\frac{1}{2}$×OB•xA,即$\frac{1}{2}$×5•|xP|=$\frac{3}{2}$×$\frac{1}{2}$×5×4,
解得:xP=6或xP=-6,
∴点P的坐标为(6,-1)或(-6,11).
点评 本题主要考查待定系数法求一次函数解析式,待定系数法求一次函数解析式一般步骤是:
(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
16.已知关于x的方程x2+(2m-3)x+m2=0有两个实数根x1,x2,且x1+x2=x1•x2,则m=( )
| A. | m=-3或1 | B. | m=1 | C. | m=-3 | D. | m=-3且m≠0 |
10.点(4,-3)是反比例函数y=$\frac{k}{x}$的图象上的一点,则k=( )
| A. | -12 | B. | 12 | C. | -1 | D. | 1 |
17. 如图,钟面上的时间是8:30,再经过t分钟,时针、分针第一次重合,则t为( )
如图,钟面上的时间是8:30,再经过t分钟,时针、分针第一次重合,则t为( )
 如图,钟面上的时间是8:30,再经过t分钟,时针、分针第一次重合,则t为( )
如图,钟面上的时间是8:30,再经过t分钟,时针、分针第一次重合,则t为( )| A. | $\frac{75}{6}$ | B. | $\frac{150}{11}$ | C. | $\frac{150}{13}$ | D. | $\frac{180}{11}$ |
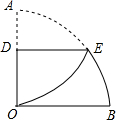 在扇形纸片AOB中,∠AOB=90°,OA=4,将扇形纸片AOB按如图所示折叠,使对折后点A与点O重合,折痕为DE,则$\widehat{BE}$的长度为$\frac{2}{3}$π.
在扇形纸片AOB中,∠AOB=90°,OA=4,将扇形纸片AOB按如图所示折叠,使对折后点A与点O重合,折痕为DE,则$\widehat{BE}$的长度为$\frac{2}{3}$π.

 如图,已知点C在线段AB的延长线上,AC=16cm,AB=6cm,点D是线段AB的中点,点E是线段BC的中点,求线段DE的长度.
如图,已知点C在线段AB的延长线上,AC=16cm,AB=6cm,点D是线段AB的中点,点E是线段BC的中点,求线段DE的长度.